Russell's paradox

Russell's paradox, discovered by Bertrand Russell in 1901, was a paradox with set theory as it existed at the time. It struck at the heart of set theory and to some extent mathematics itself. This led to significant changes in set theory and the general formalisation of mathematics.

As an introduction, we will look at a simple paradox developed by Russell himself to help explain Russell's paradox. We will then look at main problem and the most widely accepted resolution.

The barber's paradox

The barber of a small village claims that he shaves every man in the village who doesn't shave himself and that he doesn't shave anyone else.

This might seem a reasonable claim as he is the only barber in the village.

But the question is, does he shave himself? That creates a paradox. If he doesn't shave himself, that contradicts the statement that he shaves every man who doesn't shave himself. If he does shave himself, then it contradicts the statement that he doesn't shave any man who does shave himself.

In fact, not everyone regards this as a paradox. One interpretation is that the barber simply didn't think to include himself as a special case. The barber either shaves himself or doesn't, and he probably does, because who else would do it? Maybe the fact that he shaves himself was too obvious to mention.

But when we apply this to the mathematical properties of sets, it is a bit more difficult to wriggle out of.

Sets

Russell's paradox applies to sets, so it is worth recapping exactly what a set is, in mathematical terms. A set is a collection of things. Pretty much any well-defined collection of things that can be a set. We can have sets of numbers:

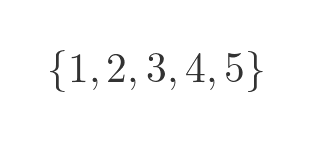
Or a set of letters:

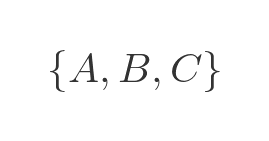
Or a set of shapes

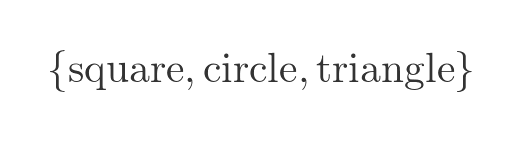
We don't even have to list the items individually, we can simply describe the criterion using a set comprehension. This notation says that the set contains all x for which x is an integer between 1 and 5 inclusive (it is the same set as the set of numbers, above, just defined by a condition):

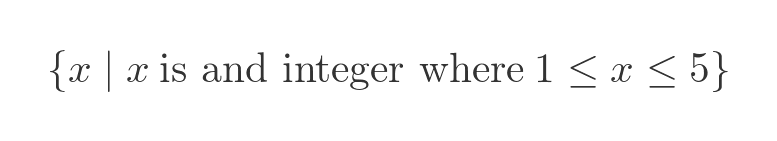
This allows us to specify sets that are too long to conveniently list:

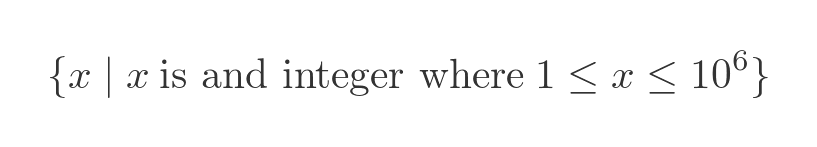
We can also specify infinite sets in this way, which is very useful. We can't list all the natural numbers, but we can still define the set containing them all:

Can a set contain other sets? Of course, why not? For a set S, we could define a set that contains all the subsets of S. This is called the power set of S. For {1, 2, 3} this set is:

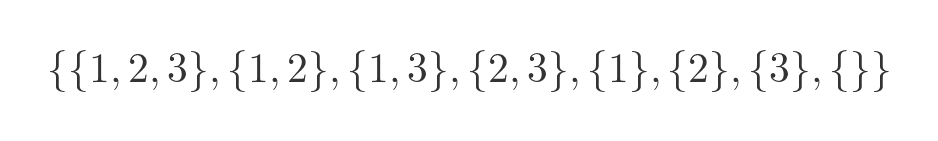
Notice that the power set contains the original set and the empty set.

Here is a more tricky question. If a set can contain sets, can it contain itself? Sure, why not? A set can contain anything, after all. The simplest example is the universal set - the set that contains all sets:

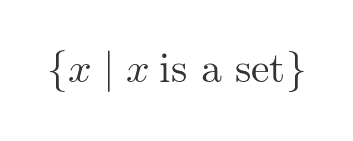
Since this set contains all sets, and it is a set itself, then of course it contains itself. But it isn't the only set that contains itself.

The set of all sets that contain at least one element contains itself. So is the set of sets that contain at least two elements. And so on.

We can also define sets that explicitly contain themselves:

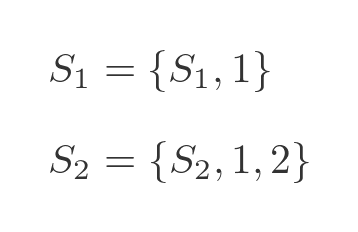
Russell's paradox

Russell's paradox is similar to the barber's paradox (he deliberately designed the barber's paradox as an illustration). It concerns the following:

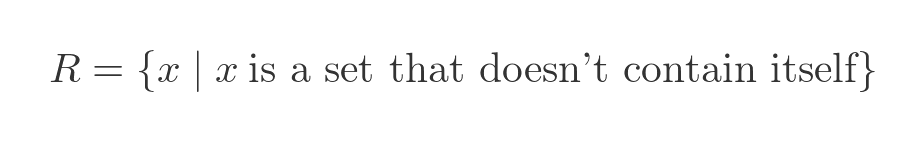
The question is, does R contain itself?

If R isn't a member of R, it means that R is a set that doesn't contain itself. So R should be a member of R.

But if R is a member of R, it means that R is not a set that doesn't contain itself. So R should not be a member of R.

This is a similar paradox to the Barber's paradox. The difference here is that we have made a statement about sets, and R is definitely a set. We can't use the excuse that R is some kind of special case like we did with the barber.

Consequences of Russell's paradox

At the time, set theory was seen as a foundation for several important areas of mathematics, including abstract algebra, and group theory, amongst others.

Russell's paradox created something of a crisis in set theory. If the theory could lead to paradoxes, how could it be trusted? And that in turn appeared to dash any hopes of unifying those other areas

This led to several attempts to patch up the theory, most of which were not successful.

Set theory at the time is now referred to as naive set theory (it wasn't called that at the time, of course, back then it was just set theory). Naive mainly refers to the idea that you can define any set you wish, using natural language. While, in practice, this works most of the time, it has a serious flaw - it permits paradoxical definitions.

The theory that is currently favoured by most mathematicians is Zermelo-Fraenkel set theory, known as ZF. This is a theory based on a rigorous set of axioms, rather than the vaguer definitions of naive set theory.

ZF set theory

Ernst Zermelo proposed the first axiomatic set theory in 1908, in response to the various paradoxes that had been discovered in naive set theory. This theory was improved in the early 1920s by Abraham Fraenkel and others, to form ZF set theory.

The theory includes ten axioms that provide a formal basis for set theory. These axioms didn't completely change set theory, but they did remove a few incorrect assumptions that were present in naive set theory. For Russell's paradox, the important Axiom of restricted comprehension.

Naive set theory included a dangerous assumption. We might now call this the Axiom of unrestricted comprehension, although again it wasn't called that at the time. It wasn't a recognised axiom, in fact, it wasn't even recognised as an assumption. It was the idea that we can define a set however we like, using natural language. This allowed us to do crazy things like defining a set that has itself as a member, without even questioning it.

ZF theory limits this in an important way. We can define a set using any rules we like to select elements from an existing, valid set. For example, if we start from the set of natural numbers we can define a rule to obtain the set of even numbers:

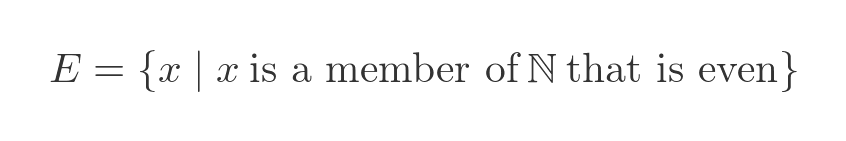
We can obtain the set of numbers that have a letter "y" in them when written in English:

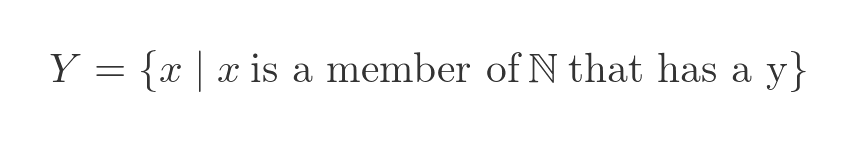
We can even write a nonsense rule like the set of numbers that are cats. Of course, this is an empty set:

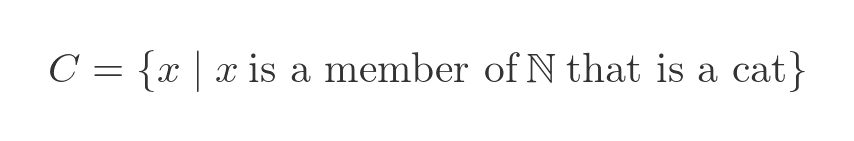
We can also write a rule that selects all the natural numbers that are not in the set of natural numbers, which again will be the empty set:

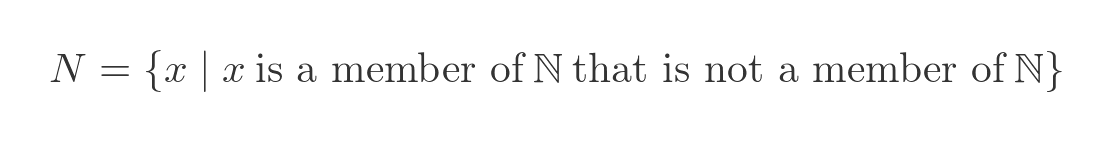
Because we are always selecting from an existing valid set, there is no possibility of a recursive rule creating a paradox. The Russell paradox set can't be written as it is, because it needs a rule that selects a subset of an existing set:

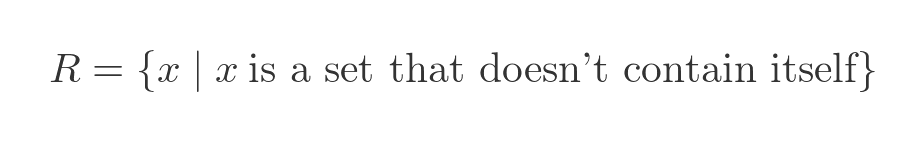
To write this in terms of a set, we would need to do this:

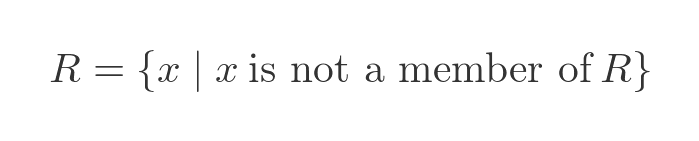
But that isn't allowed because we must use an existing set. We can't use R to create R, because at the time of creation R doesn't yet exist.

What if we deliberately tried to create a paradox? Suppose we define a set Q in terms of R and then use that to define R:

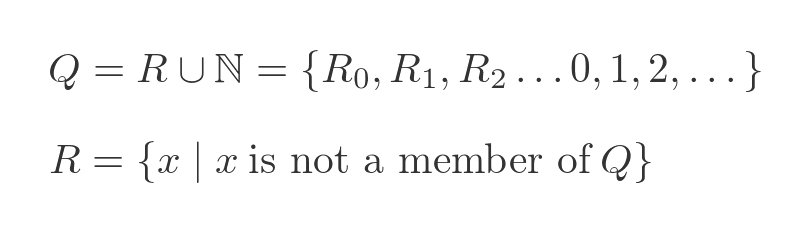
This won't work either, because we can't create Q before R exists and we can't create R before Q exists, so we can't create a set this way.

In summary, the ZF theory says that Russell's paradox doesn't occur because it uses an invalid method of constructing a set.

What about the barber's paradox

So where does that leave us on the barber's paradox? Well, let's define two groups:

Based on what we have learned so far, we can write the original formulation of the barber's paradox - the barber shaves every man who doesn't shave himself - like this:

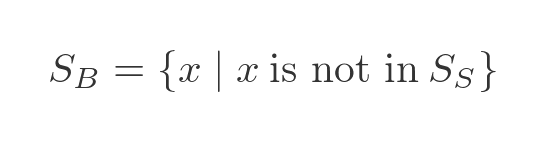
We are asserting that the men who are shaved by the barber are the exact same group as the men who don't shave themselves. So we can write this equation purely in terms of the men who are shaved by the barber:

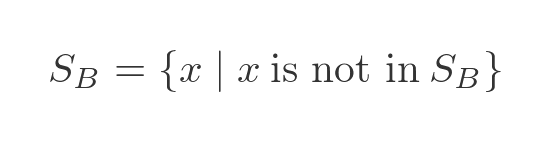
This, of course, is the paradox. But under ZF we don't allow this set. So what happens instead?

First it will be useful to create another set, the set of men who do not shave themselves:

ZF does allow us to construct a set from individual elements. So we could define our three sets by simply listing everyone in the village who belongs to each set. Here are the three groups:

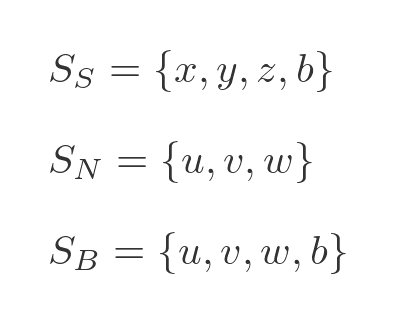
For the sake of argument, we are assuming that the barber does shave himself. So the men who shave themselves are some of the villagers (represented by x, y and z) and the barber (b). The men who do not shave themselves are the rest of the villagers (represented by u, v and w). The men the barber shaves are u, v, w, and himself. There is no possibility of paradox here, we have simply listed every man in each group.

Now we have our statement that the barber shaves every man who doesn't shave himself. Looking at the groups above, we can see that this clearly isn't true. It isn't a paradox, it is just plain wrong:

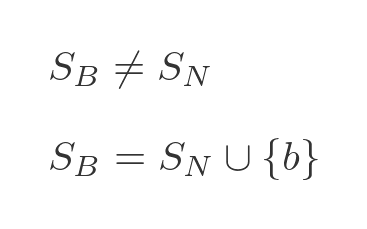
The truth, as written above, is that the barber shaves every man who doesn't shave himself, AND in addition he also shaves himself.

Suppose the barber doesn't shave himself. We then have three slightly different sets. The barber is now placed in the set of people who don't shave themselves, and the set of people the barber shaves is now just u, v and w:

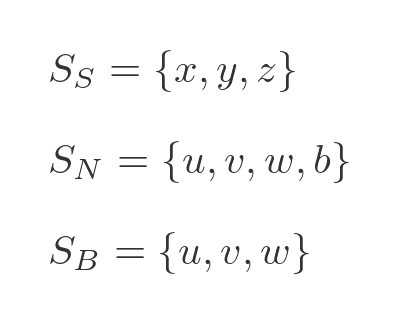
This time the statement that the barber shaves every man who doesn't shave himself is still incorrect, just in a different way:

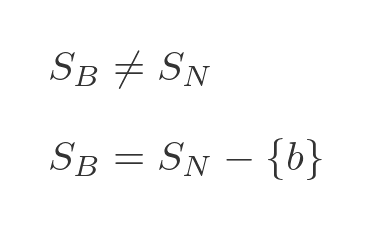
This time the correct statement is that the barber shaves every man who doesn't shave himself, EXCEPT THAT he doesn't shave himself.

See also

• Monty Hall problem
• Pigeonhole principle
• Drunk man and keys problem
• Raven paradox
• Painter's paradox
• Potato paradox
• Coin rotation paradox