Potato paradox

The potato paradox is a very simple paradox, but many people find it quite surprising, and confusing, or might even refuse to believe it.

Suppose you buy 100 kg of potatoes. Potatoes contain water, of course, and these particular potatoes contain 99% water.

Overnight, some of the water in the potatoes evaporates, so by the morning, the potatoes contain 98% water. How much do the potatoes now weigh?

What was your answer?

Many people guess 99 kg or similar.

The actual answer is 50 kg!

Veridical paradox

A common response is that this isn't a true paradox, it is simply a counterintuitive fact. But, in fact, it is an example of a veridical paradox - a result that is undoubtedly true, but many people find it hard to believe.

The confusion usually arises because we tend to look at the change in the proportion of water, from 99% to 98%, and jump to the conclusion that the amount of water lost is equal to 1% of the total mass. But that isn't correct. It isn't even close.

A moment's thought proves that the answer of 99 kg can't possibly be true. Initially, there is 99 kg of water out of a total mass of 100 kg, so the water percentage is:

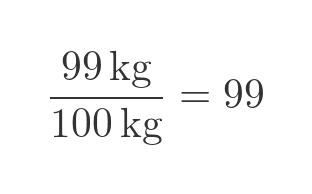
If there was 98 kg of water out of a total mass of 99 kg, the water percentage would be:

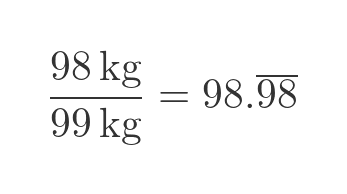
So the percentage of water wouldn't be 98%, it would still be very nearly 99%.

Mental model

The essence of this paradox is that it misdirects you into a flawed mental model of what is going on.

The problem seems very simple, so we might not feel it requires a lot of thought. We tend to assume that the total mass of the potato can't have changed by much (because the water content, the main component of its mass, appears to have only changed by 1%). This offers an easy and intuitive solution, so our brain glosses over the fact that this would require some of the water to magically transform into potato solids (which is obviously impossible).

Some people complain that the scenario is unfair or unrealistic. For one thing, real potatoes aren't 99% water. While that is true, however, potatoes do contain quite a lot of water. If you have ever found an old potato that perhaps rolled to the back of the store cupboard and dried out, you will see that it genuinely is far smaller than its original size.

The other part of the problem that might be misleading is that potatoes don't generally shrivel to half their size overnight. So again, that part of the setup encourages you to imagine that the potato won't have changed very much, which could be seen as slightly underhand. Regardless of that, though, if you work through the basic maths then the correct answer is easy to derive.

The main misdirection is that it focuses your attention on the water. If we concentrate on the potato solids instead of the water the result is clear.

A better way of viewing the problem

Let's reframe the problem, and think about the dry content of the potato.

At the start, we have x amount of potato solids that make up 1% of the total mass. In the end, we still have x amount of potato solids, but it now makes up 2% of the total mass. How has the total mass changed?

Here, the top set of squares represents the 100 kg of potato of which 1% is solid potato (the single dark green square) and 99% (the 99 light blue squares) is water:

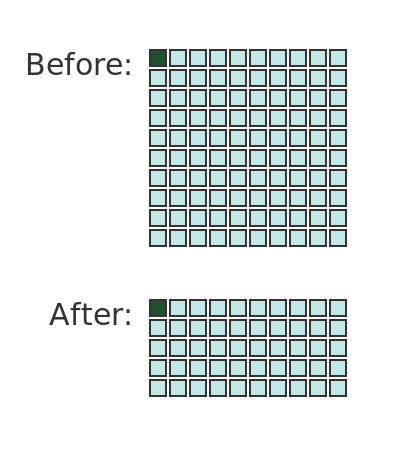
If we remove water until the single green square represents 2% of the total mass, then clearly we must halve the total mass, as the bottom set of squares illustrates.

Or just use algebra

This problem can also be solved with straightforward algebra. Let's say that the mass of the potato solids is x, the mass of the water is w, and the total mass is t. The fraction of the potato that is water is given by f (eg if the potato is 99% water, f will be 0.99).

Looking at the initial state we know that the total mass is the sum of the mass of the water and the mass of the potato solids:

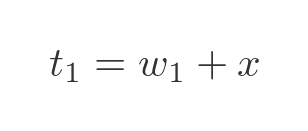
We've used the suffix 1 to indicate the initial state before drying out. We also know that the water mass is the total mass multiplied by the water fraction, f:

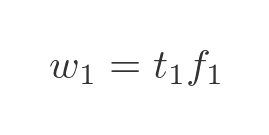
Combining and rearranging these expressions gives us:

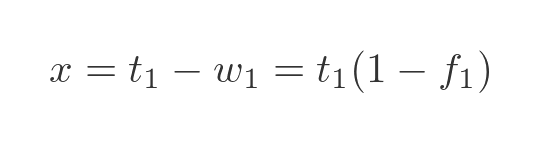
So we can find the total mass in terms of the potato mass and the fraction:

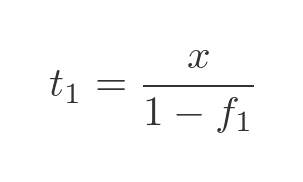
The total mass after drying can be calculated in the same way using the second set of values (with suffix 2). Notice. of course, that the value x is unchanged:

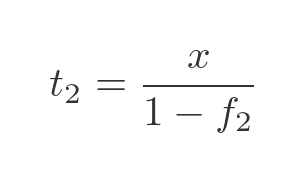
Now we can calculate the ratio of the total mass after drying vs the original total mass:

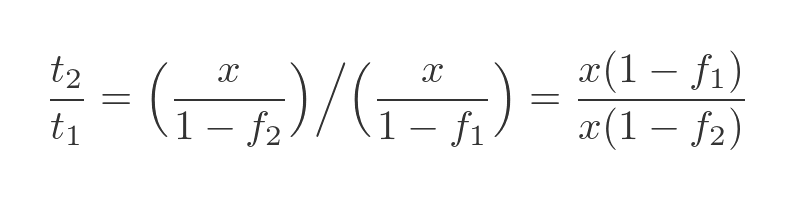
The x terms cancel out. We also know that f1 is 0.99 and f2 is 0.98, so the mass ratio is:

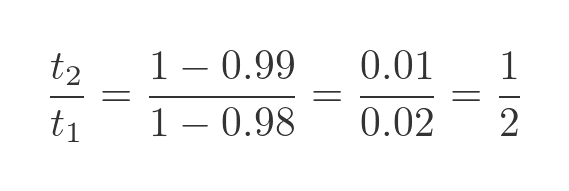
Proving that, after drying, the potatoes have half their original weight.

A related problem

Another well-known problem, that is tricky in a similar way, is the bat and ball problem.

It goes like this. A toy bat and ball cost \$1.10 in total. If the bat costs \$1 more than the ball, how much does the ball cost?

A surprising number of people, including people who might generally be regarded as being quite good at maths, will immediately answer 10c. Even though it is obviously not correct (if the ball is 10c, the bat would be \$1.10, so the total would be \$1.20).

It works in a similar way to the potato paradox. The problem itself appears very simple, so you aren't encouraged to think about it too much. And a quite plausible value for the bat price, $1, appears right there in the question. So there is a good chance that someone might answer with that poorly thought-out guess.

Again, some simple algebra gives the correct answer. If the ball costs x and the bat costs t, then the total cost must add up to \$1.10:

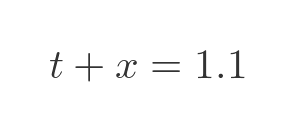
And the bat costs \$1 more than the ball:

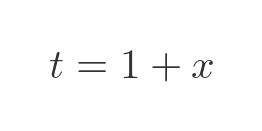
Substituting t is the first formula gives:

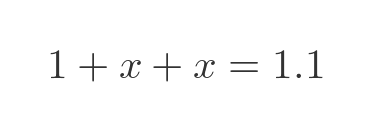
So of course the ball costs \$0.05 and the bat costs \$1.05.

See also

• Monty Hall problem
• Pigeonhole principle
• Drunk man and keys problem
• Raven paradox
• Painter's paradox
• Russell's paradox
• Coin rotation paradox