Monty Hall problem
Categories: recreational maths paradox

The Monty Hall problem is a famous (or infamous) mathematical paradox that has caused many arguments over the years. It isn't actually a paradox at all, it is just a probability calculation that many people find non-intuitive when they first meet it.
Gameshow
The paradox is based on a US game show from many years ago, called Let's Make a Deal, hosted by Monty Hall.
At one point in the show, the contestant has the opportunity to win a car. They have a choice of three doors (labelled 1, 2 and 3). There is a car behind one of the doors and nothing behind the other two doors. The contestant chooses a door. They have no idea which door leads to the car, of course.
After they have made their choice, the host Monty will open one of the other two doors. Monty knows where the car is, and he will always open a door that contains no prize.
At this point, there are two doors still unopened. The contestant now has a choice - they can stick with the door they originally picked, or they can change their mind and switch to the other door that Monty didn't open.
What should they do?
A non-intuitive result
Most people initially think that it makes no difference which door the contestant chooses.
Their reasoning is as follows. When the player originally chooses a door, the car is either behind that door or it isn't. Monty Hall opening a different door makes no difference to where the car is, so how can it be any better or worse to swap?
The truth is that if the player swaps doors they are twice as likely to win the car.
Why is this true?
There have been many explanations of this problem, some of them quite complex, involving thought experiments where there are 1000 doors, among other things. I hope this description is simpler.
Let's look at a couple of possible scenarios. First, let's assume the car is behind door 2. The contestant (let's personalise this and say that you are the contestant) incorrectly guesses door 1.
Then Monty opens one of the other doors. Monty knows that the car is behind door 2, and he must open an empty door, so he has no choice but to open door 3. Here is a diagram representing this:
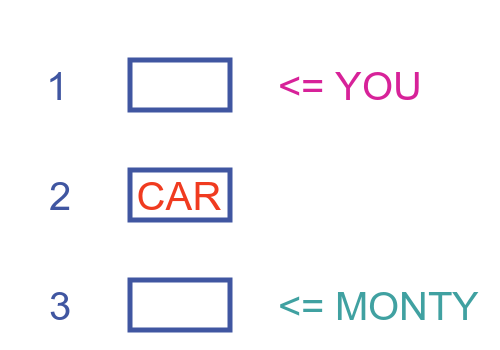
In this case, the car is behind the other door, so you are better off swapping. But, of course, you have no way of knowing this.
Now let's assume the car is behind door 3. This time you guess door 3. You got lucky, but you don't know it.
Now Monty opens a door that has no car behind it. In this case, he could open either door, because the car isn't behind either of them. Let's assume he opens door 1, although it doesn't make any difference which one he chooses:
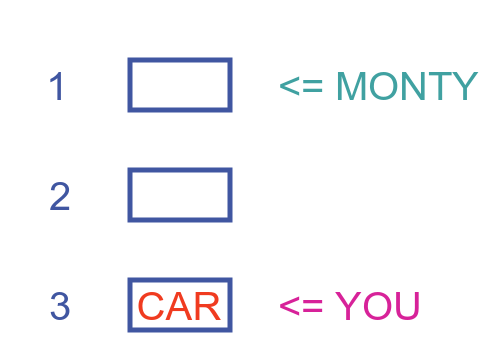
In this case, the car is behind your door, so you are better off sticking with your original choice. But once again you have no way of knowing this.
There are only two situations!
Now there are quite a lot of combinations in this problem - where the car is, which door you choose, which door Monty chooses, and whether you decide to swap. But there are only two situations. Your initial guess can either be right or wrong:
- If you guess the correct door, the car will definitely be behind your door, so you shouldn't swap.
- If you guess the wrong door, the car will definitely be behind the remaining door (after Monty has opened the other door), so you should swap.
Those are the only two possible cases. Your initial guess determines whether the car will be behind your door or the other door. Everything else is just a distraction.
Of course, you have no way of knowing if your guess was correct.
But what you do know is that your initial guess is more likely to be wrong than right, because you are picking one door out of three. There is a 2/3 chance that your guess is wrong, and only a 1/3 chance it will be right.
So if you always act as if you guessed wrong, you will win more often than you lose. You should swap doors.
This only works because Monty has insider info
If Monty didn't know where the prize was, the situation would be completely different. In that case there would be three equally likely possibilities:
- The car is behind the door you choose.
- The car is behind the door Monty reveals. That would spoil the game, of course, because you would have no chance of winning.
- The car is behind the other door.
If Monty reveals a door that doesn't have a car behind it, then the car must be behind one of the other two doors, but with equal probability. There would be no benefit is changing, because both doors are equally likely to have the car behind them.
See also

Join the GraphicMaths Newletter
Sign up using this form to receive an email when new content is added:
Popular tags
adder adjacency matrix alu and gate angle answers area argand diagram binary maths cartesian equation chain rule chord circle cofactor combinations complex modulus complex polygon complex power complex root cosh cosine cosine rule cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon eigenvalue eigenvector ellipse equilateral triangle euler eulers formula exercises exponent exponential exterior angle first principles flip-flop focus gabriels horn gradient graph hendecagon heptagon hexagon horizontal hyperbola hyperbolic function hyperbolic functions infinity integration by parts integration by substitution interior angle inverse hyperbolic function inverse matrix irrational irregular polygon isosceles trapezium isosceles triangle kite koch curve l system line integral locus maclaurin series major axis matrix matrix algebra mean minor axis n choose r nand gate newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutations polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral questions radians radius rectangle regular polygon rhombus root sech segment set set-reset flip-flop sine sine rule sinh sloping lines solving equations solving triangles square standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations trapezium triangle turtle graphics variance vertical volume volume of revolution xnor gate xor gate