Pigeonhole principle

Imagine you have nine boxes, represented by the nine squares below. You also have ten items, represented by the red dots.

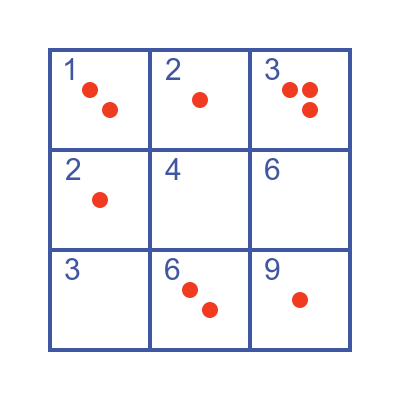
You must put each object into one of the boxes. You can put each object into any box you want, and each box can hold as many objects as you like. There are, of course, many different ways to do this. For example, for each item you might pick a box at random and put the item in that box. It might look something like this:

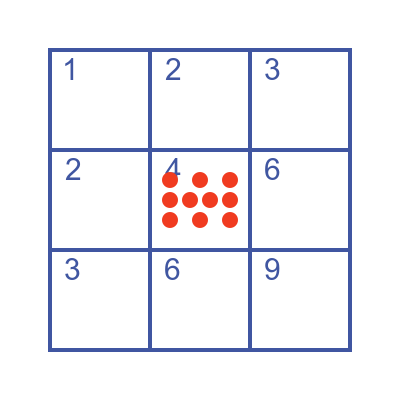
Or you might just put all ten items in box 4, like this:

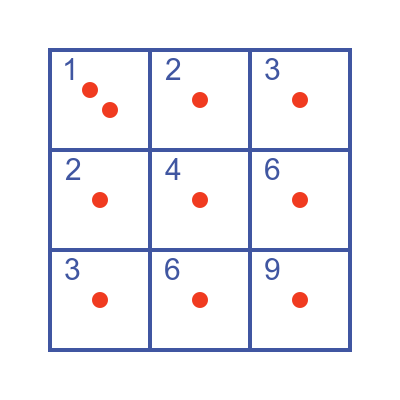
Or you could put the first item in box 1, the second item in box 2, and so on. Of course, after nine items you would run out of boxes so you might put the final item in box 1:

The pigeonhole principle says that, if you have n boxes, and m items, where m > n then however you choose to arrange the items in the boxes, at least one box will contain more than one item.

It seems obvious

The principle seems pretty obvious. There are more items than there are boxes so every item cannot have its own box. So at least one box must have more than one item.

However, obvious as it is, it can sometimes tell us things that are quite surprising.

A classic example

We can prove there are at least two people in London who have the same number of hairs on their heads!

How can we prove that? Well, the average person has about 100,000 hairs on their head. People don't typically have more than 150,000 hairs. We will assume that nobody has more than a million hairs.

The population of London, in 2023, is about 9.5 million people.

If we took those 9.5 million people and placed each person in a figurative box according to how many hairs they have on their head, we would be putting 9.5 million objects in 1 million boxes, so at least one box would have more than one person in it.

The interesting thing about this proof is that it is practically impossible to count all the hairs on someone's head. Counting the number of hairs on 9 million people's heads is even more difficult. And when you consider that we lose about 100 hairs a day, which is about one every 15 minutes, then we would need to count every hair on 9 million people's heads within the same few minutes otherwise the counts would all have changed.

So without the pigeonhole principle, if someone asked you if two people in London have exactly the same number of hairs on their heads, you might say "Possibly, but how could we ever know?"

But with the pigeonhole principle we can prove that it is definitely true.

What the pigeonhole principle can't tell you

There are many questions the pigeonhole principle can't answer.

It can't tell you:

• Who the two people are who have the same number of hairs on their head.
• How many hairs those two people have on their heads.
• Whether anyone has exactly 103,745 hairs on their head (there probably is someone but there might not be).
• Whether anyone in London has the same number of hairs as you.

Although, as we will see later, the fact that there are 9.5 million people but only 1 million boxes, we can say for certain that there are actually at least 10 people who have the same number of hairs.

Rolling a dice

Suppose you roll a six-sided dice multiple times, and record the result in a table. For example, if you threw 5, 4, 1, 4 the table would look like this:

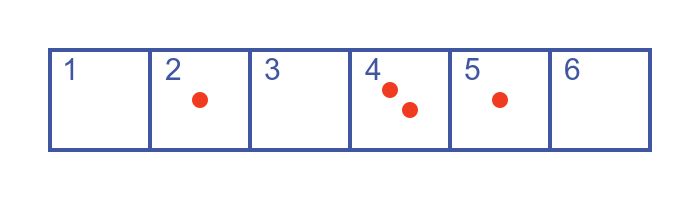
The question is how many times would you need to roll the dice to guarantee that you would get the same number more than once?

The way to think of this is that each roll of the dice creates an "item", and we place that item in a box determined by the value of the throw. There are six boxes, so according to the pigeonhole principle if we throw the dice seven times, at least one of the boxes must have more than one item in it. In other words, we must throw the same number twice.

This example is useful because throwing a dice is a random event, so many problems involving dice are statistical in nature. For example, we can calculate the probability of throwing two sixes in a row.

The pigeonhole principle instead deals with certainty - if we throw the dice seven times, at least two of those throws will land on the same number.

If we were to ask instead, how many times must we roll the dice to guarantee that we throw a six more than once, then the pigeonhole principle won't help us. It can tell us with certainty that at least one number will occur at least twice in seven throws. But it is impossible to say how many times you must roll the dice to get two sixes specifically. You might roll the dice a hundred times and never get a six at all (it is highly unlikely but certainly possible).

Extending the principle

Returning to our original example of nine boxes, suppose we had 19 objects to place in those boxes. We choose the number 19 because it is 2x9 + 1.

In that case, the pigeonhole principle would tell us that at least one box must contain more than two items.

Why is that true? Well if we add 18 items to the nine boxes like this we can avoid any box having more than two items:

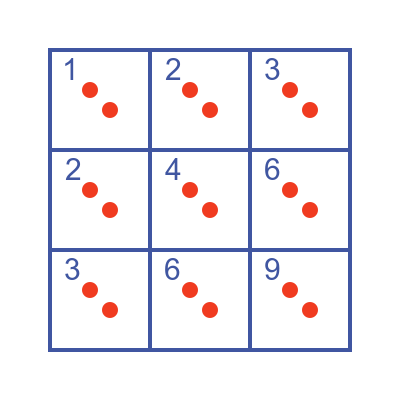
But if we add a 19th item, there is no possible way to do that without at least one box containing three items.

Notice as well that this is all the principle tells us. It doesn't tell us anything about the other boxes. In the example above one box has three items and the other boxes all have two items, but that doesn't have to be the case. For instance, we could have put all 19 items in one box and left all the other boxes empty.

In general, for if we have n boxes and m items, and m > kn for some integer k, then at least one box must contain more than k items.

In the case of the number of hairs example, n is 1 million, m is 9.5 million, therefore m > 9n (ie k = 9) so there must be at least 10 people who have the same number of hairs on their heads.

Number of handshakes

Here is another example. If there is a gathering of people, and some of them shake hands with each other, then at least two of those people must have taken part in exactly the same number of handshakes.

We can prove this using the pigeonhole principle, but it isn't completely obvious.

Let's assume there are 10 people. This means that each person can shake hands with up to 9 people. But some people might not shake hands at all. So there are 10 possibilities for how many hands each person can shake: 0, 1, 2 ... 9.

So we have 10 items (the people) and 10 boxes they could be placed in (according to how many hands they shook, 0 to 9). Which would seem to imply that they could all have shaken a different number of hands.

But this would be missing an important fact. If someone didn't shake hands with anyone, then nobody else could have shaken hands with everyone. And if someone shook hands with everyone, then everyone else must have shaken hands with at least one person.

It is therefore impossible for someone to have shaken hands with 0 people and also for someone else to have shaken hands with 9 people. So:

• If someone hands with shook hands with 0 people, box 9 must be empty, so 10 people must fit into 9 boxes (0 to 8).
• If someone hands with shook hands with 9 people, box 0 must be empty, so 10 people must fit into 9 boxes (1 to 9).
• If neither of those is true, boxes 0 and 9 are empty, so 10 people must fit into 8 boxes (1 to 8).

This means that we are placing 10 people into 9 boxes, so at least one box must contain more than one person. So at least two people must have shaken hands the same number of times.

A Putnam question

The William Lowell Putnam Mathematical Competition is an annual competitive maths examination, known for posing difficult questions. Here is a question from 2002:

A sphere has 5 distinct points on its surface. Prove that at least four of those points lie in the same closed hemisphere.

This problem can be solved using the pigeonhole principle. Here is the sphere with the five points marked:

We start by choosing any two points. We can draw a great circle through these points. A great circle is a diameter of the sphere, that divides it into two equal hemispheres. It is always possible to draw a great circle through any two distinct points on the surface:

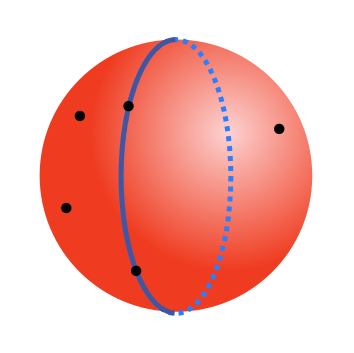
Each of the remaining three points will be in one of the two hemispheres. Since there are three points and only two hemispheres, it follows from the pigeonhole principle that one of the hemispheres must contain at least two of the points.

We choose the hemisphere containing at least two points, and make that a closed hemisphere:

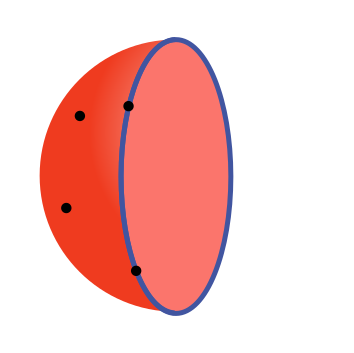
The closed hemisphere contains the points on its boundary so that hemisphere contains at least 4 points, which is what we set out to prove.

Of course, it is possible that the great circle passes through three or more of the points. If it passes through three points, then we simply need to select a hemisphere containing at least one of the other points to ensure that the hemisphere contains at least four points. If the great circle passes through four or five points, then of course either hemisphere will contain at least four points.

See also

• Monty Hall problem
• Drunk man and keys problem
• Raven paradox
• Painter's paradox
• Potato paradox
• Russell's paradox
• Coin rotation paradox