Coin rotation paradox

Imagine we have 2 coins. The radius of the larger coin is 3 times the radius of the smaller coin.

We roll the smaller coin all the way around the edge of the larger coin, without it slipping:

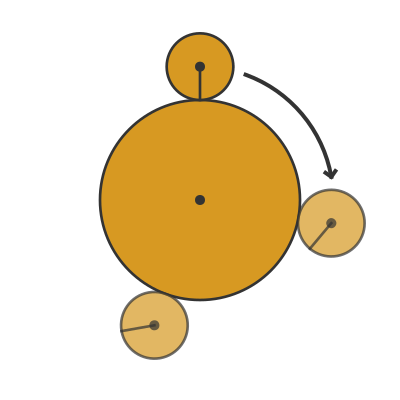
The question is, how many times will the smaller coin rotate as it rolls around the edge of the larger coin?

The result might not be quite what you expect, and in this article, we will look at a couple of explanations why. In addition, we will explore how this paradox relates to astronomy!

The "obvious" answer

If the circumference of the smaller coin is C, then the circumference of the larger coin must be 3C, since the circumference is proportionate to the radius.

This means that to rotate around the larger coin, the smaller coin must cover a distance of 3 times its circumference, which means it must rotate 3 times.

But that isn't what happens!

Here is an animation of what really happens:

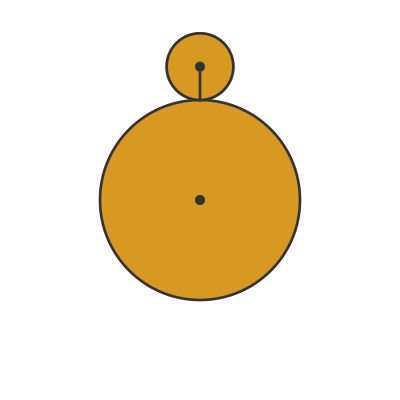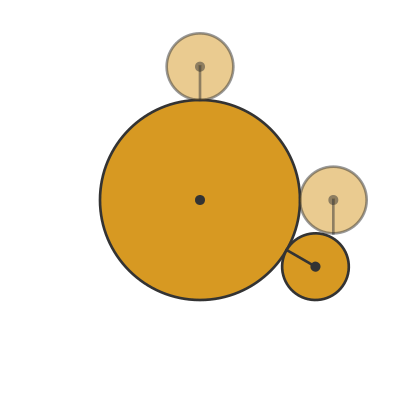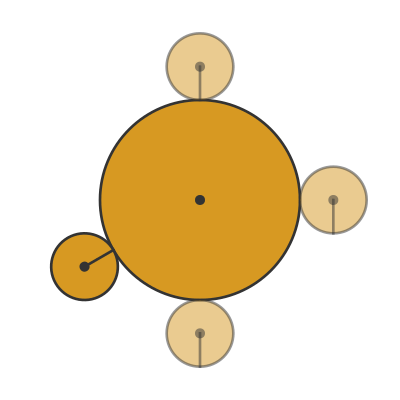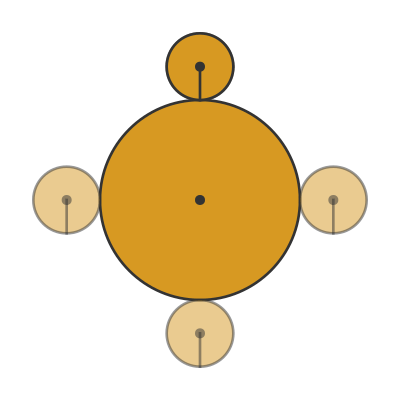
The small coin actually rotates 4 times before it returns to its initial position.

This might seem very strange. If the bigger coin has 3 times the circumference of the small coin, and the small coin rotates without slipping, how can it possibly take 4 rotations to get back to its starting point?

But it really does. This isn't a trick animation, if you try it with real coins, you will get the same effect. And as we will see, this is also well-known effect in astronomy.

Whatever the relative sizes of the coins, the small coin always rotates one more time than you might expect. If the small coin was a quarter of the size of the big coin, it would rotate 5 times. If it was half the size it would rotate 3 times. If both coins were the same size it would rotate twice.

We will look at 2 different resolutions to this paradox.

Resolution 1 - rolling around a circle adds an extra rotation

This first resolution is the one that I find to be the more intuitive explanation. It is based on the observation that, from the point of view of the large coin, the small coin does rotate 3 times. We can see that here:

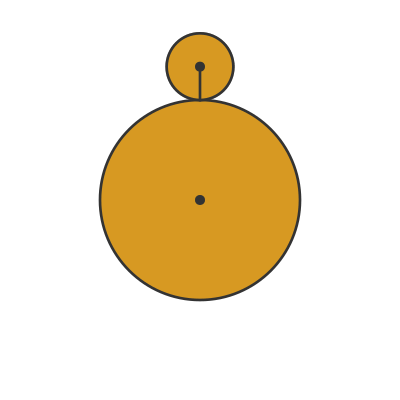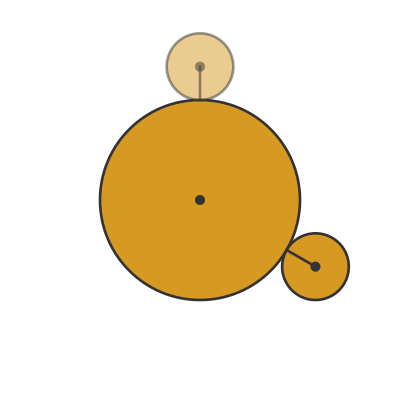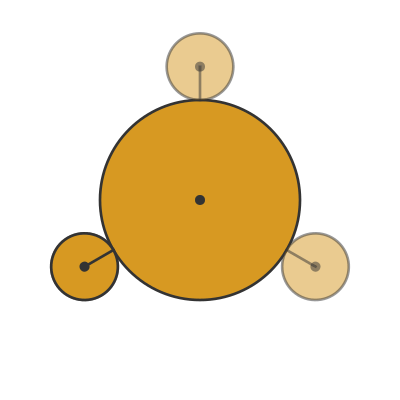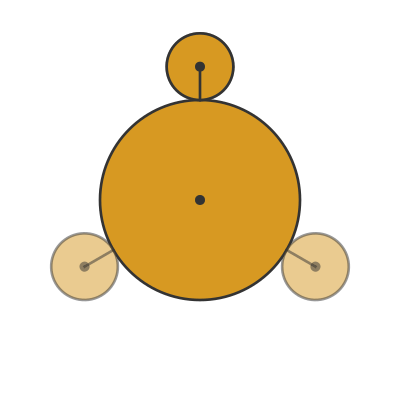
The small coin is drawn with a black line that initially points towards the centre of the large coin.

From the point of view of the large coin, the small coin will have completed a full rotation when the black line once again points to the centre of the large coin. This happens after 120 degrees, then again after 240 degrees, and finally after a full rotation of 360 degrees.

So from this viewpoint, the small coin rotates 3 times, and each rotation corresponds to the coin rotating along one-third of the large coin's circumference. So there is no paradox here.

But when we look at the situation from an external observer, we see one extra rotation. Why is that? Well, it is because while rolling along the edge of the large coin, the small coin also moves in a large circle.

We can separate this movement. Let's take away the large coin, and instead place the small coin on a turntable. The coin is completely stationary relative to the turntable:

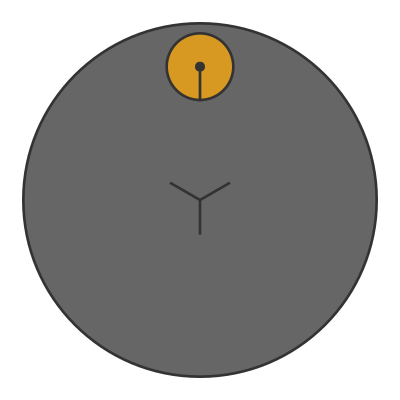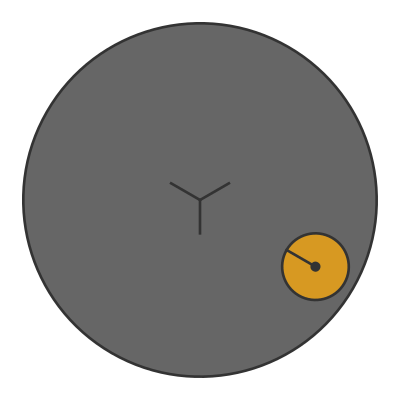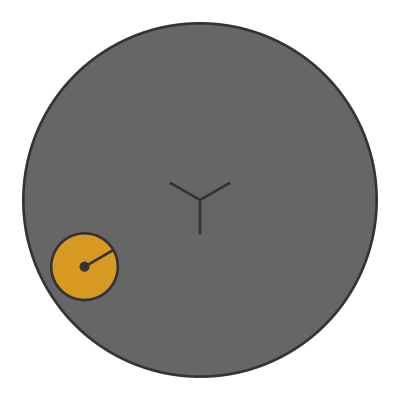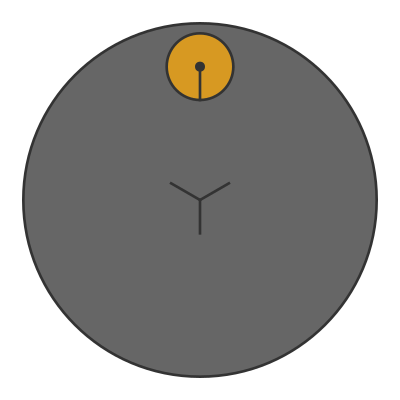
At the start, when the coin is at the top of the image, the line on the coin is pointing straight down. After the turntable has rotated by 90 degrees, the line on the coin is pointing to the left. After another 90 degrees, the coin is at the bottom of the image and the line is pointing straight up, and so on.

By the time the turntable gets back to its start position, the coin has effectively rotated by a full turn about its centre.

The combination of these two effects means that the coin will have rotated 4 times rather than 3.

Resolution 2 - only the distance travelled by the coin centre matters

This diagram shows what happens if we roll the small coin along a flat surface:

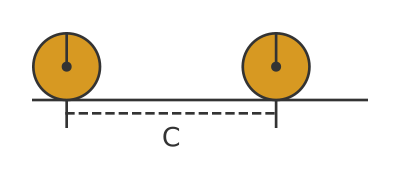
The circumference of the coin is C. This means that if the centre of the circle moves a distance C, and the circle doesn't slip, the circle must rotate exactly 1 full turn.

We can say that if the centre of a circle, circumference C, rolls without slipping by a distance C, the circle must rotate exactly one full turn.

If we apply this principle to the rotating circle, it looks like this:

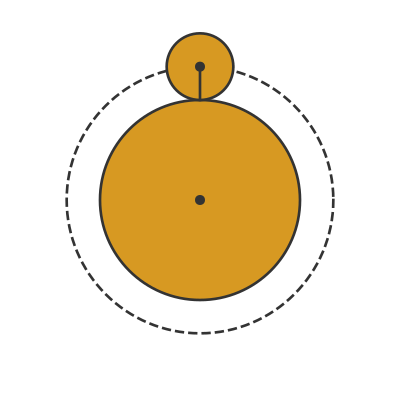
The small coin has a radius of r and a circumference of C. The large coin has a radius of 3r.

The centre of the small coin moves along the dotted circle. The radius of that circle is r plus 3r, a total of 4r. This means that the circumference of the dotted circle is 4C.

Since the centre of the small coin is travelling a distance of 4C, it must rotate through 4 complete turns.

This still feels slightly unsatisfactory to me. The centre is moving by 4C, but the edge is only rolling over a curve of length 3C. How does that work?

Rolling around a polygon

We can gain an intuition (though not proof) by looking at what happens when we roll a coin around a square. The animation below shows a square with side length C (again, the circumference of the coin):

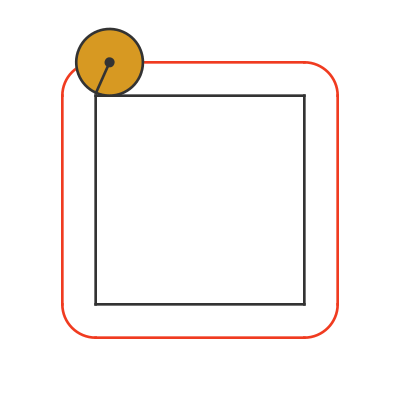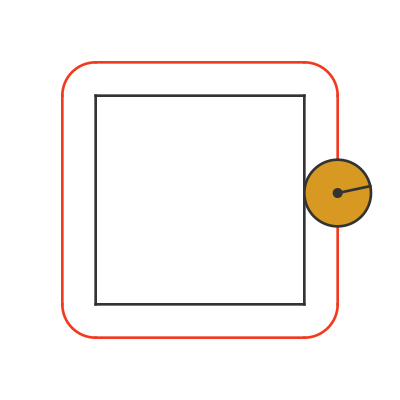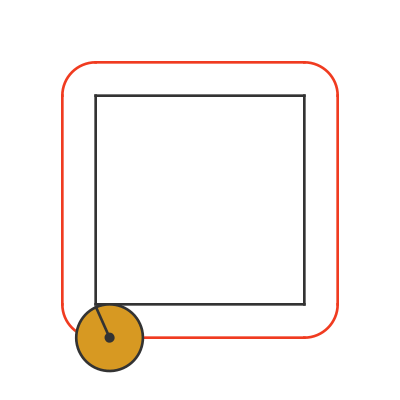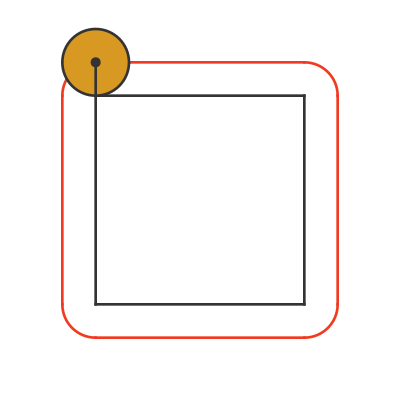
The red line shows the path that the centre of the coin takes around the square.

Let's consider one of the straight edges first. As the coin rolls along one edge of the square, it rotates exactly one time (because the side length is C). Notice also that the straight part of the red curve is the same length as one side of the black square.

Now look what happens at the corner. The coin pivots over the corner, through 90 degrees. The part of the coin that is in contact with the square doesn't move, but the coin doesn't slide, it just pivots.

On each corner, the centre of the coin takes a circular path. It is a quarter circle, and the radius is equal to the coin radius. After going around the complete square, the 4 rounded corners will add up to a complete circle, with the same radius as the coin.

So in summary, the coin will have turned through an extra full rotation (in addition to the rotations it makes while rolling along the edges). And the path taken by the coin centre is exactly C longer than the combined lengths of all the sides that the coin rolls around. But without the coin slipping.

This is the exact behaviour we saw when rotating the coin around a larger coin, but in this case, the behaviour is explained because the coin pivots over each corner.

Here is what happens with an octagon:

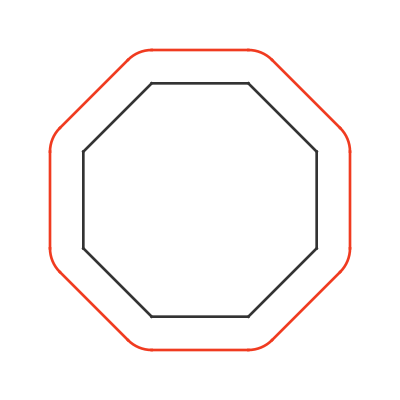
This time there are 8 sides and 8 arcs. Each arc is an eighth of a turn, so again the arcs add up to a full circle. The effect is the same as the square - the path of the centre of the coin travels a distance C more than the perimeter of the shape, and the coin pivots through an extra 360 degrees. But it happens in 8 steps rather than 4.

If we increase the number of sides to 16 the pattern continues:

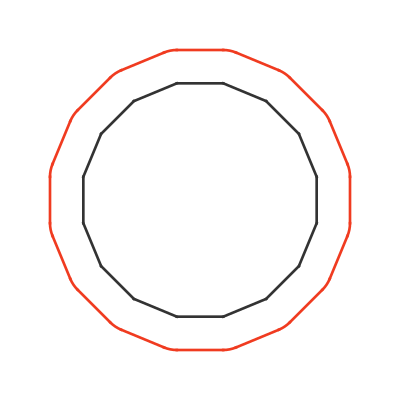
As the number of sides increases, the length of each side decreases and the size of each arc decreases. Eventually, the shape tends towards a circle, so the extra distance and angle are added continuously rather than stepwise.

So enough of coins, let's move on to something a bit bigger. Our solar system consists of round objects the spin on their own axes while rotating around other round objects, and the same rules apply. We will slightly simplify the description here, assuming that our solar system is all in one plane, but that doesn't make too much difference to the result.

Example - the moon

As the Moon orbits the Earth, we always see the same side, the near side. We never see the "dark" side of the Moon. From our perspective, the Moon doesn't rotate. Similarly, if you stood on a part of the Moon where the Earth is directly overhead, then the Earth would always be directly overhead.

Here is a diagram of this:

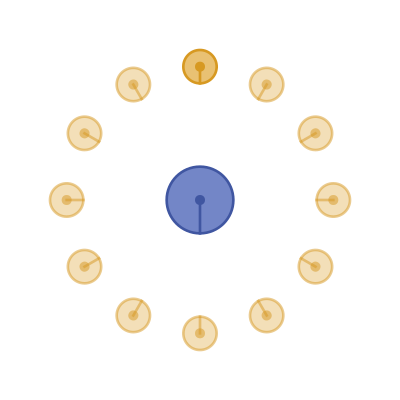
The reason we see the same side of the moon all the time is that the moon itself rotates on its axis exactly once during the time it takes to orbit the Earth. It takes about 27.332 days for the Moon to orbit the Earth, and it takes exactly the same time for the Moon to spin once on its axis.

The two time periods aren't just close, they are pretty much identical. Even if they differed by 0.1% we would see the Moon rotating very slowly (it would take almost 40 years for the Moon to make half a turn so we would see its opposite side). That doesn't happen. This is no coincidence, of course, it is caused by tidal locking.

Example - sidereal time

The Earth, as we all know, has a 24-hour day and takes approximately 365.25 days to orbit the Sun.

But we are observing this from the Earth. If aliens were observing our planet from far outside our solar system, then wouldn't they observe the Earth rotating 366.25 times in a year?

Well, yes, of course, they would, everything we have seen so far proves it. But a year is still a year to both observers. So where does the extra day come from?

The difference, of course, is due to different definitions of a day. Here is what we on Earth think a day is:

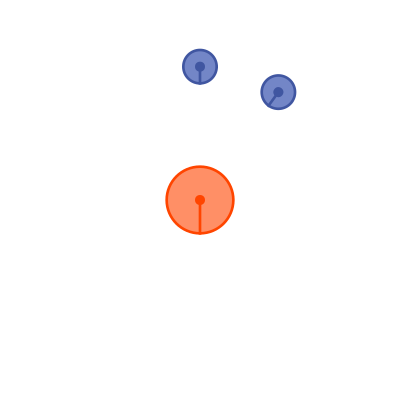
If we start the clock when the Sun is overhead, and then wait until the Sun is overhead once more, we will find that 24 hours has gone by. The diagram is exaggerated for clarity, the Earth only rotates around the Sun by about 1 degree per day.

Here is how the alien observers would measure a day:

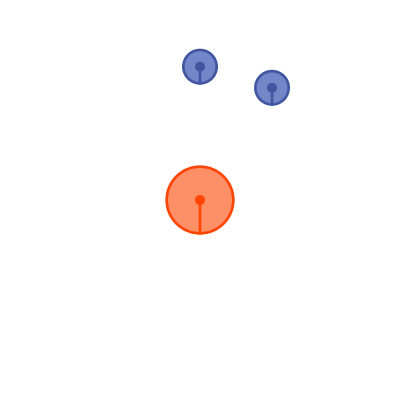
They would measure a day as one complete rotation of the Earth in their frame of reference. It takes about 23 hours and 56 minutes for the Earth to rotate on its axis. It would require an extra 4 minutes for the Earth to rotate slightly further so that the Sun was overhead once more. This is called a sidereal day, and, since this is slightly shorter than an Earth day, there are indeed 366.25 sidereal days in a year.

We can observe sidereal days from Earth, by looking at the position of distant stars. They take 23 hours 56 minutes to appear back in the same place because that is the actual time it takes for the Earth to rotate 360 degrees on its axis.

The extra 4 minutes is the time required for the Sun to be overhead because the Earth has moved around the Sun slightly since the previous day.

See also

• Monty Hall problem
• Pigeonhole principle
• Drunk man and keys problem
• Raven paradox
• Painter's paradox
• Potato paradox
• Russell's paradox