Integration by parts

Finding integrals can be challenging because, unlike differentiation, we can't usually integrate a function from first principles. Instead, we usually find integrals by identifying a related differential equation and reversing it. For example, if we happen to know that the first derivative of the function f(x) is g(x), then (subject to a few conditions) we know that the integral of g(x) will be f(x).

This gives us a repertoire of standard integrals that we can use to solve problems. However, it is always useful to expand our repertoire. One way to do that is to investigate some of the rules we use for differentiating more complex expressions. These can sometimes be "reversed" to provide a new weapon in our integration armoury.

One well-known rule we use in differentiation is the product rule. The equivalent rule for integration is integration by parts. We will introduce that method in this article, with examples and a proof using calculus.

Integration by parts

Let's start by stating the rule as an indefinite integral (we will prove it later):

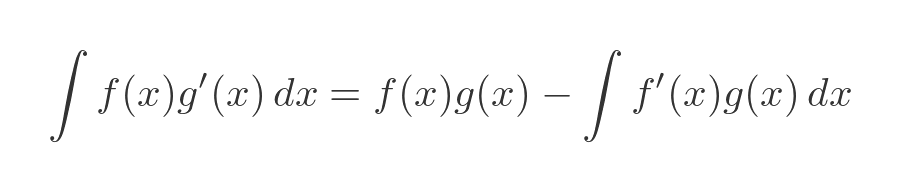
How is this useful? Well, suppose we have an expression to integrate but there is no known way to do it. But we notice that the expression is a factor of two other functions, like this:

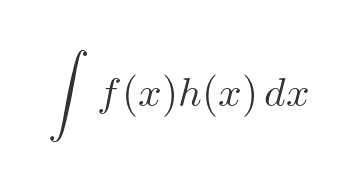
Now suppose we happen to know that the integral of h is some other function g. In other words, h is equal to g'. So now we have this:

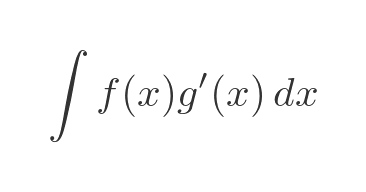
According to the formula above, we can rewrite this as:

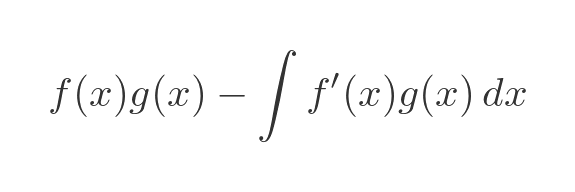
This gives us a second chance at solving the integral. It might be that f' g is easier to integrate than f g'. This sometimes happens if f' is simpler than f. And since finding f(x) times g(x) is easy (it isn't under the integral sign) we have found a solution. This doesn't always work, but it sometimes does, so it is worth a try.

Let's look at a simple example:

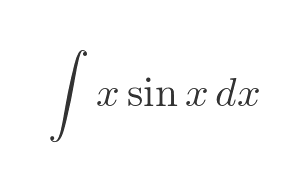
We can't integrate this directly, so we will try integration by parts. We need to split the function into two factors, one that will represent f, and the other that will represent the derivative of some other function g:

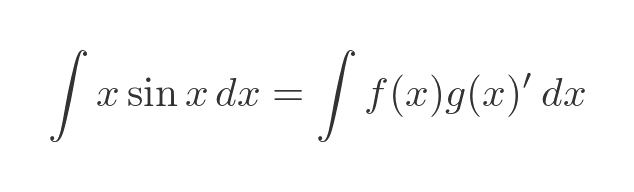
Our function can be split into two factors fairly easily, it is x times sin x. Let's try defining f and g' like this:

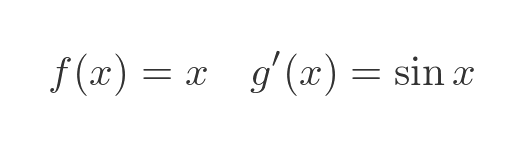
We can now find f' by differentiating f:

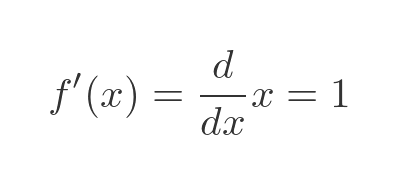
We can find g by integrating g':

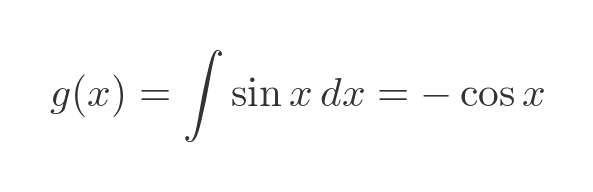
Looking back to the original rule:

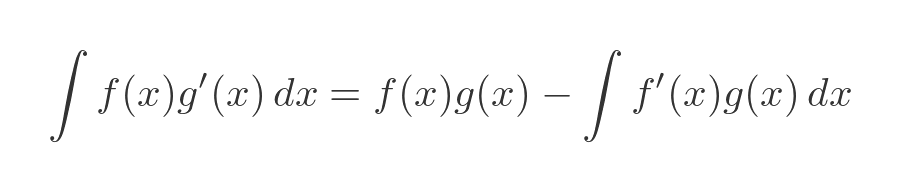
We can substitute f, g and their derivatives:

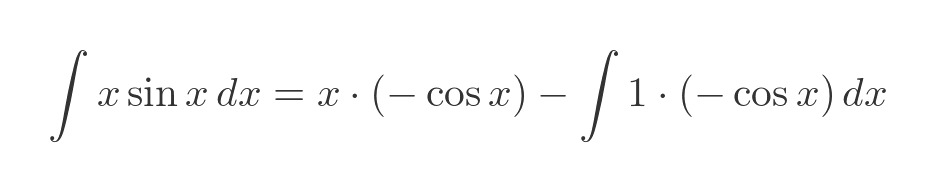
Simplifying gives:

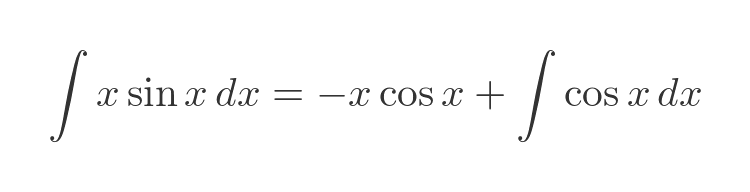
Evaluating the integral gives us the final result:

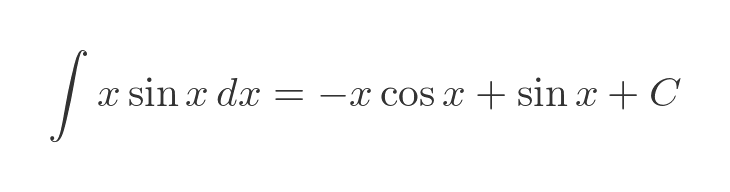
Here is a graph showing the original function on the left, and the integral on the right. As you would expect, the places where the left-hand graph is zero correspond to the turning points in the right-hand graph. Also, the regions where the left-hand graph is positive correspond to the regions where the right-hand graph has a positive slope, and vice versa. This gives us a small measure of confidence that the integral is correct:

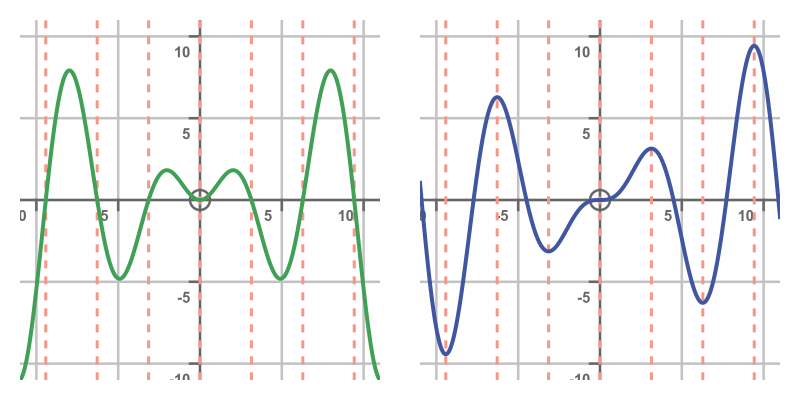
Integration by parts doesn't always work

This technique is great when it works, but in many cases (in fact most cases) it won't work. As an example, consider what might happen if we had allocated f and g' differently. In this equation:

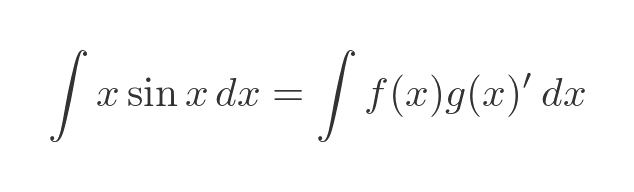
We could have chosen to swap the definitions of f and g':

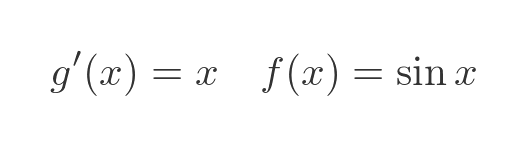
We are allowed to do this, of course, because the order of multiplication makes no difference. This would have created different f' and g functions:

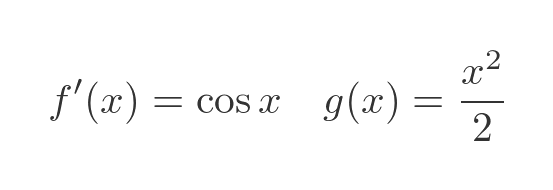
This in turn would have created a different equation for the integration by parts:

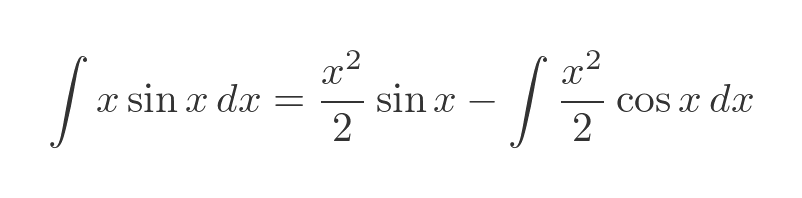
This equation is perfectly valid, but it isn't very useful because the integral on the RHS is still not solvable. If anything, it is more difficult than the original.

Standard form of integration by parts

You will often see the rule for integration by parts written in a standard, almost idiomatic, form. We will derive that form here. Taking the formula above:

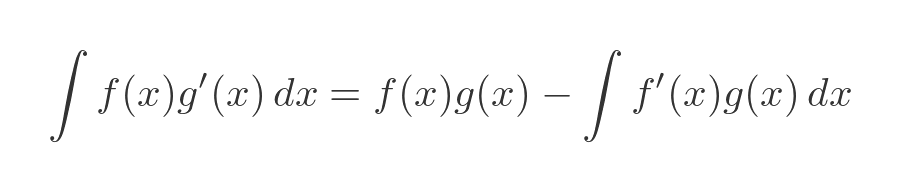
By definition, we have:

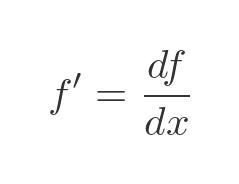
This can be rearranged to give:

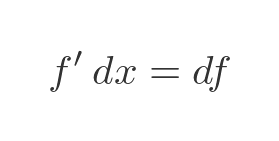
We can derive a similar result for g:

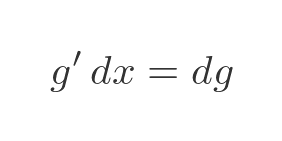
This allows us to replace dx in the original to obtain the standard formulation of the integration by parts rule:

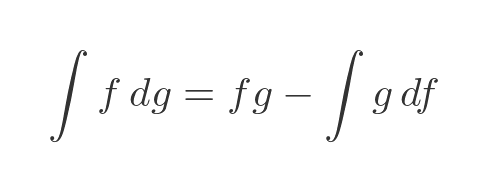
This is often written using u and v rather than f and g.

Proof

The proof of the method can be derived from the product rule of differentiation. We will assume that our functions f and g are continuously differentiable. When we say that a function is continuously differentiable, we mean that the function is differentiable everywhere and that the first derivative itself is a continuous function.

This proof assumes the product rule is already proven, see the proof from first principles here. In summary, the product rule states that, if we have a function p that is the product of two other functions:

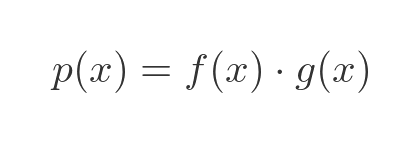
Then, using the product rule, the derivative of p will be:

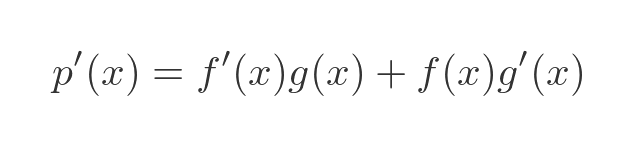
We can now integrate both sides with respect to x:

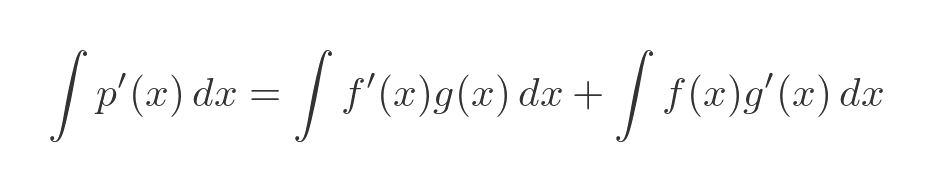
The integral of p' is just p:

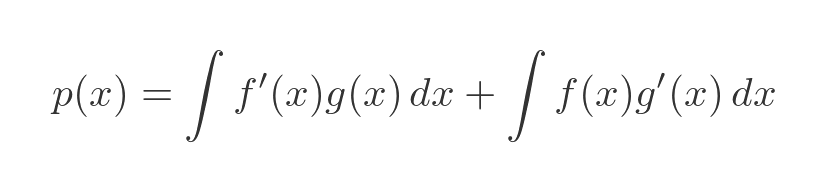
And p is the product of f and g:

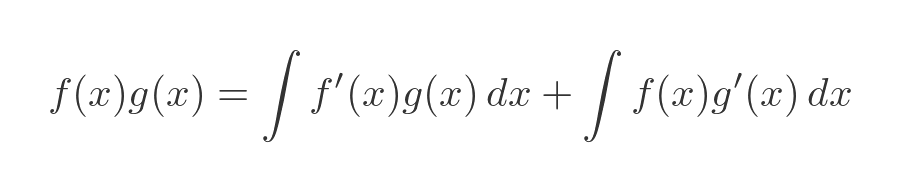
Rearranging this formula gives us the integration by parts rule:

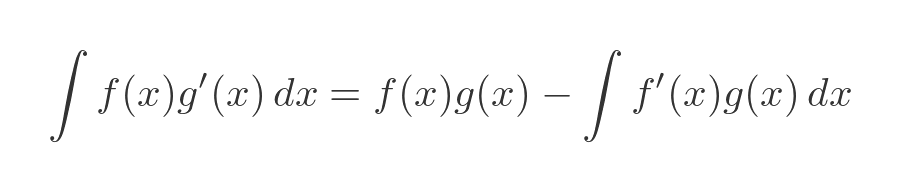
Finding the definite integral

To find the definite integral, we need to evaluate the integral term over the required range (let's call it a to b). But we also need to evaluate the product term between a and b. So:

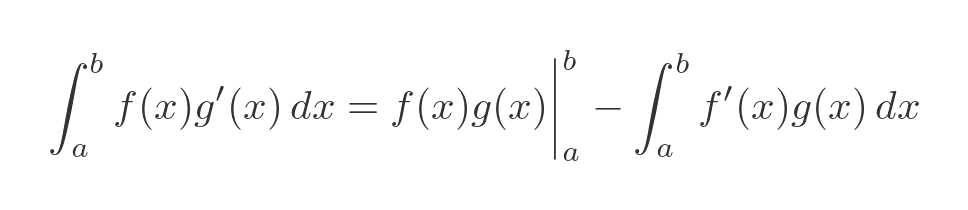
This is equivalent to:

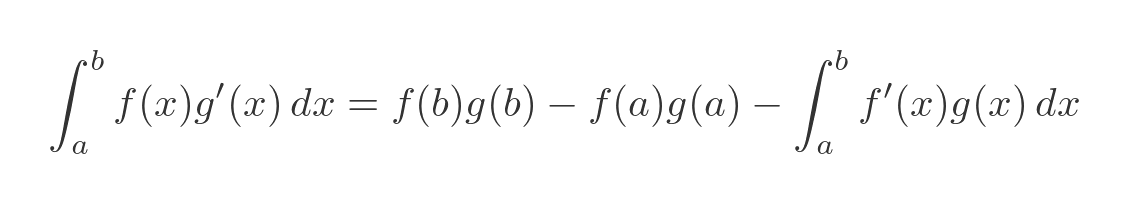
Example

As a second example, we will evaluate this definite integral:

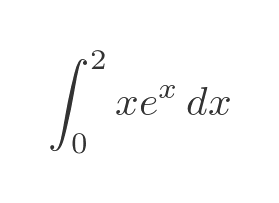
We will choose f and g' as follows:

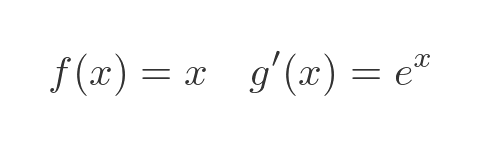
This means that f' will be 1, as in the previous example. To find g, we rely on the special property of the exponential function, that it is its own derivative. So g is the same as g':

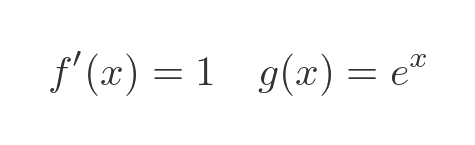
So, using the equation for the definite integral by parts we saw in the previous section, we have:

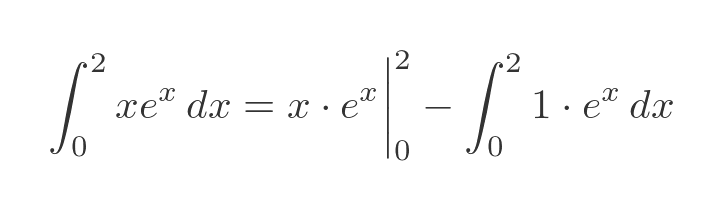
Evaluating the second integral between 0 and 2 gives:

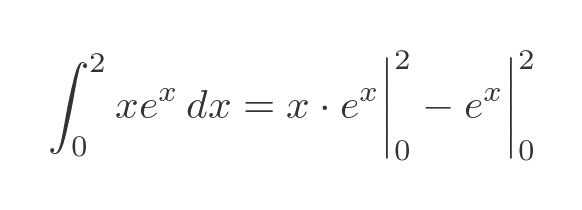
We can gather both terms on the RHS and evaluate them both between 0 and 2:

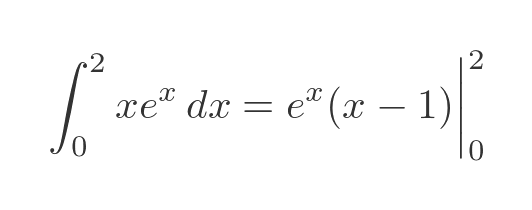
Substituting the values gives:

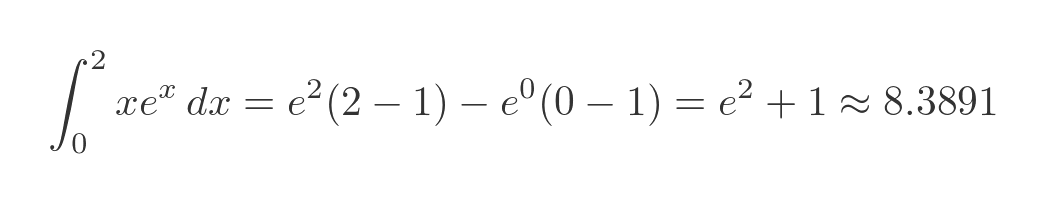
These graphs show the original function of the left, with the calculated integral on the right. The integral graph has been adjusted by adding a constant 1 to ensure that the integral starts at zero when x is zero (because the definite integral range starts at zero):

The value of the graph on the right, when x is 2, is about 8.3891 as calculated above. For the curve on the left, we would therefore expect the area under the curve between 0 and 2 to also be 0.83891.

As a quick check, the yellow triangle also has an area of 0.83891. Visually, it is certainly plausible that the area of the triangle is equal to the area under the curve, which gives an informal validation of the result.

See also

• What is integration
• Integration by substitution
• Mean value theorem for integrals
• Fundamental theorem of calculus
• Improper integrals
• Integration by parts - LIATE rule
• Finding arc length by integration
• Volume of revolution
• Gabriel's horn