Gabriel's horn

Gabriel's horn is a 3-dimensional shape with an interesting and seemingly paradoxical property. It has a finite volume but an infinite surface area.

This leads to an apparent paradox called the painter's paradox that was covered in this article. The paradox arises because the shape can be filled with a finite amount of paint (since it has a finite volume). But when it is full, the paint must be touching every part of its inner surface. Since the surface area is infinite, this implies that we have covered an infinite area with a finite amount of paint! See the linked article for a resolution to this paradox.

In this article, we will prove that the shape has finite volume and infinite area. We will do this in two different ways, first using an infinite series of cylinders (similar to the way the problem was first solved by Evangelista Torricelli in the 17th century), and then using calculus.

Gabriel's Horn

Let's start with the definition of Gabriel's horn (you may already be familiar with this if you have read the previous article). The shape is based on this function:

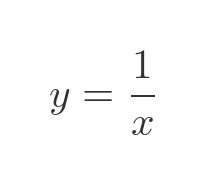
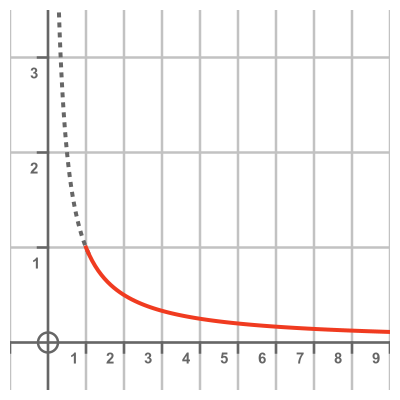
To create Gabriel's horn, we take the part of the curve where x is greater than or equal to 1:

We then rotate the shape around the x-axis to form a surface of revolution:

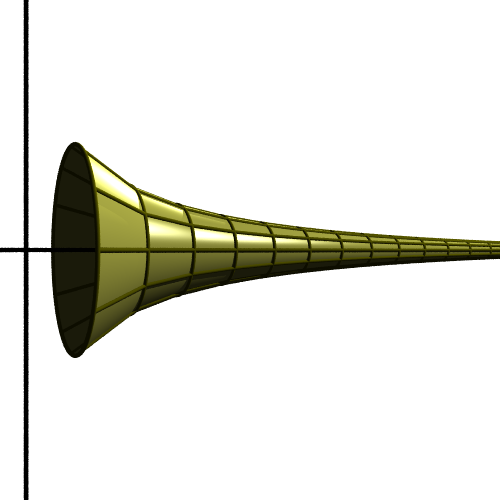
This horn is infinitely long because the original function never reaches 0. But it gets narrower and narrower and we travel along the x-axis in the positive direction.

Proving that the volume is finite

The obvious way to find the volume of the shape is to use integration to find the volume of revolution. However, that is not the only way to prove it is finite. Torricelli proved the result without the use of calculus. The method we will look at here is similar to Torricelli's method, but modified and simplified. It is mentioned in this wikepedia article and described in more detail in this nice Mathologer video.

To prove the result, we first create a step function that is always greater than or equal to the inverse function:

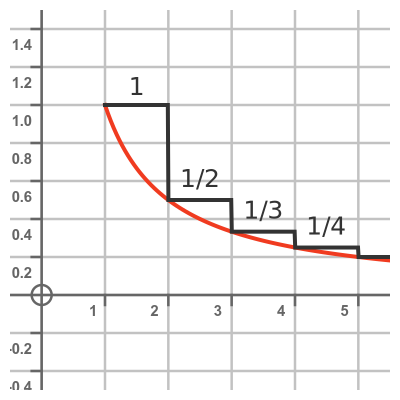
For x between 1 and 2, our step function has a value of 1, which is also the value of the horn function when x is 1. For x between 2 and 3, our step function has a value of 1/2, which is the value of the horn function when x is 2. The next step has a value of 1/3, then 1/4, and so on forever.

If we rotate the step function around the x-axis (just like we did to create the horn), each step creates a cylinder:

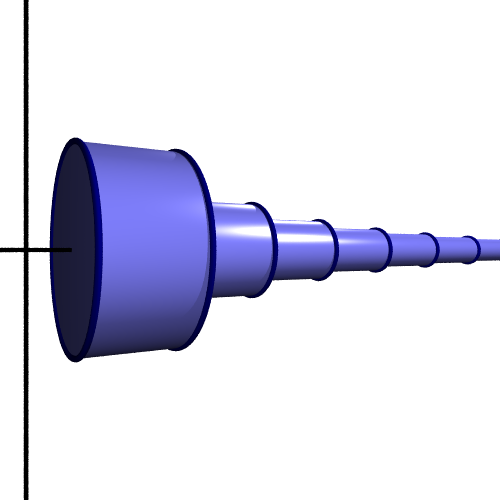
The first step creates a cylinder of radius 1. The next has a radius of 1/2, the next has a radius of 1/3 and so on. Now, since the step function is always greater than or equal to the inverse function, it follows that the rotated horn shape will be enclosed within the cylinders:

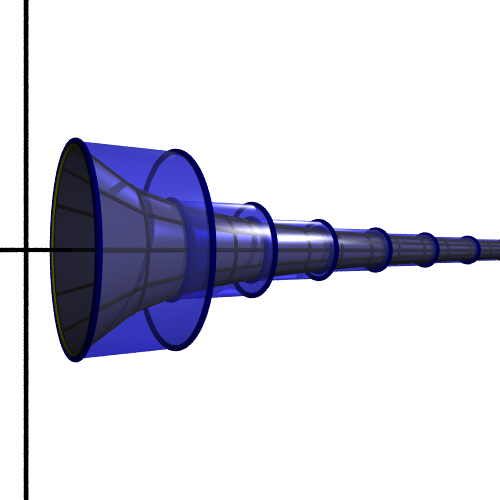
This means that the volume of the horn is less than the volume of the cylinders. So if we can prove that the volume of the cylinders is finite, we have also proved that the volume of the horn is finite. We will prove this now.

The volume of a cylinder is a standard formula:

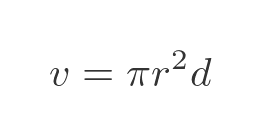
Where r is the radius and d is the height of the cylinder (which is the width, as it is drawn above). Noting that all our cylinders have a width of 1 this simplifies to:

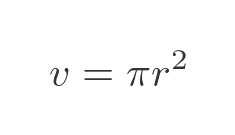
Now, the first cylinder has a radius of 1, the next has a radius of 1/2, then 1/3 and so on. So the total volume of all the cylinders is:

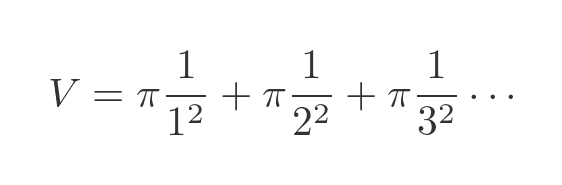
Taking out a common factor of π gives:

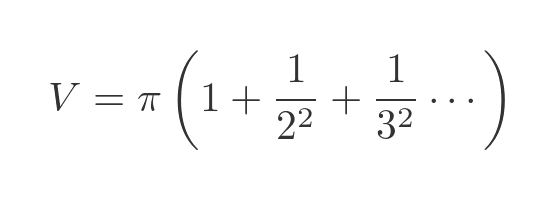
The term in brackets is the infinite sum of inverse squares, which is a well-known sum known as the Basel problem. Its value was calculated by Euler. The result is a little strange because it involves the square of π, but what is more important to us is that it is a finite value.

Since this volume is greater that the volume of Gabriel's horn, this proves that the volume of Gabriel's horn is also finite!

Proving that the surface area is infinite

We take a similar approach to the surface area. But since we are expecting it to be infinite, we start with a step function that is enclosed by the horn function:

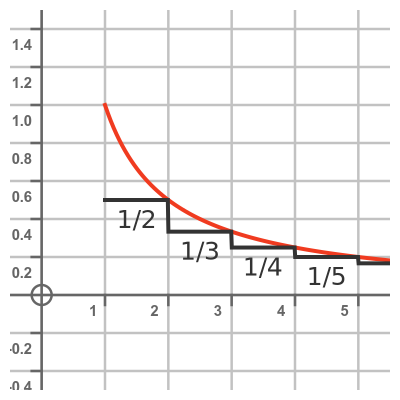
For x between 1 and 2, our step function has a value of 1/2, which is also the value of the horn function when x is 2. For x between 2 and 3, our step function has a value of 1/3, which is the value of the horn function when x is 3. The next step has a value of 1/4, then 1/5, and so on forever.

Again, if we rotate this about the x-axis we get a set of cylinders:

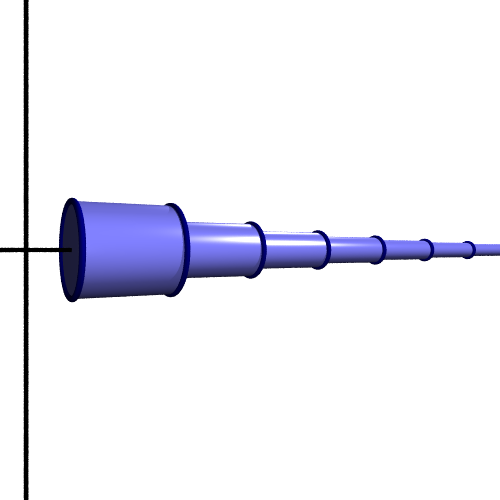
The first step creates a cylinder of radius 1/2, then 1/3, then 1/4 etc. This time, since the step function is always less than or equal to the inverse function, it follows that the rotated horn shape will enclose the cylinders:

We will be comparing the surface area of the horn with the sum of the surface areas of the edges of all the cylinders. We will ignore the areas of the two circular faces of each cylinder.

Looking at the first cylinder and comparing it to the corresponding part of the horn, the cylinder has a constant radius of 1/2. The section of the horn has a radius that varies between 1 and 1/2. The radius of the horn is always greater than or equal to the radius of the cylinder, therefore the surface area of the horn in that section must be greater than the surface area of the cylinder. That is true for every section of the horn, so the overall surface area of the horn is greater than the combined surface area of all the cylinders.

So if we can prove that the surface area of the cylinders is infinite, we will have proved that the surface area of the horn is infinite.

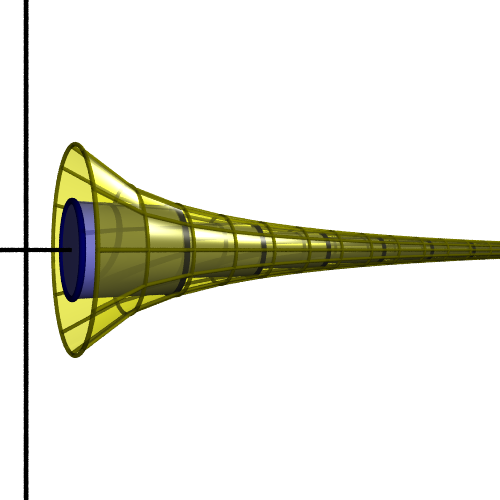
The surface area of the edge of one cylinder, again where r is the radius and d is the height, is given by the standard equation:

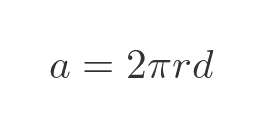
Again, all our cylinders have a width of 1 so this simplifies to:

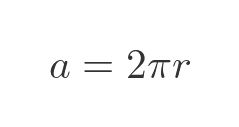
Now, the first cylinder has a radius of 1/2, the next has a radius of 1/3, then 1/4 and so on. So the total area of all the cylinders is:

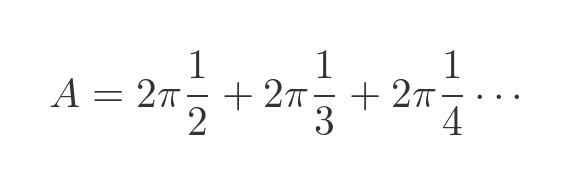
Taking out a common factor of 2 π gives:

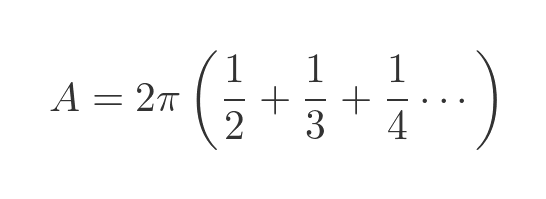
The series in brackets, the sum of all the integer fractions, is known as the harmonic series, and it is well known that it diverges (ie it has an infinite sum). Strictly speaking, the harmonic series starts with 1, then 1/2, 1/3 etc. So our equation is 1 less than the sum of the harmonic series, but of course, infinity minus 1 is still infinity, so the surface area of the cylinders is infinite.

This proves that the surface area of Gabriel's horn is also infinite.

Proofs using calculus

Gabriel's horn is a solid of revolution created by rotating the function 1/x around the x-axis. There is a standard formula for calculating the volume of this shape, for a general function f(x). We won't prove it here (that is a topic for a different article), we will just state that the volume of the 3D solid between a and b is:

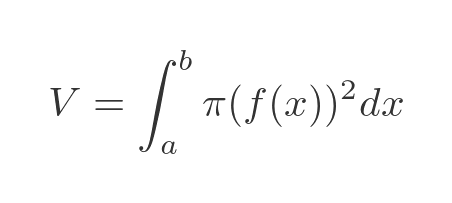
The surface area of the solid is given by:

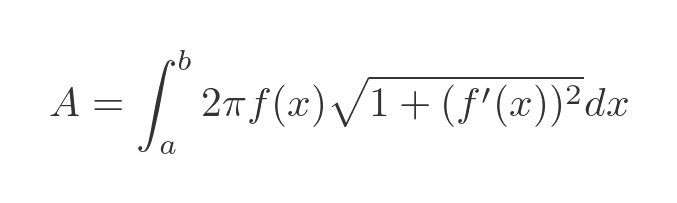
One other thing we need to consider is that we are trying to find the value of these integrals between 1 and infinity. An integral with a limit of infinity is called an improper integral and we can't evaluate it simply by plugging the value infinity into the normal equation for a definite integral. Instead, we must first calculate the definite integral up to some finite limit b and then calculate the limit of the result as b tends to infinity:

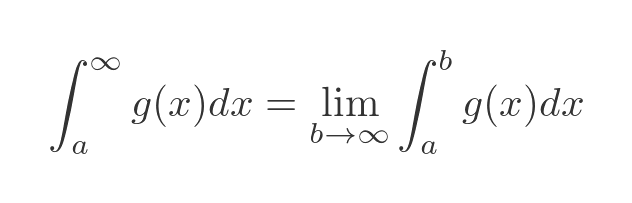
Proving finite volume using calculus

We can calculate the horn volume using the volume integral above, with the function 1/x, over the range 1 to infinity. As discussed above, we express the improper integral as a limit:

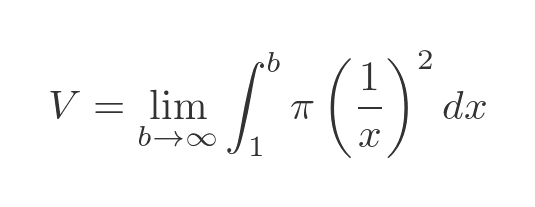
Simplifying and taking π outside the integral gives:

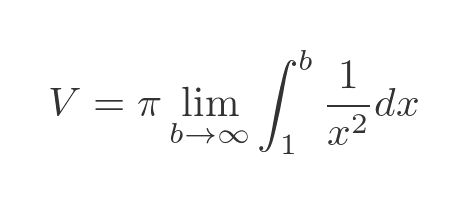
We use the standard integral:

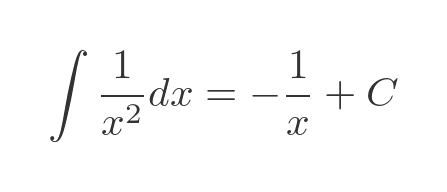
And evaluate between 1 and b:

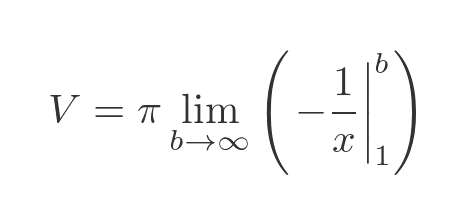
This gives:

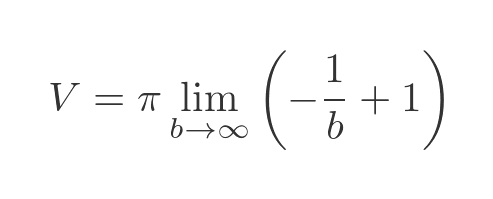
As b tends to infinity, 1/b goes to 0 so the final result is simply:

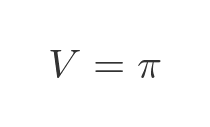
This proves that the volume is finite, and as a bonus, we know its exact value.

Proving infinite surface area using calculus

We can also calculate the horn volume using the area integral from above:

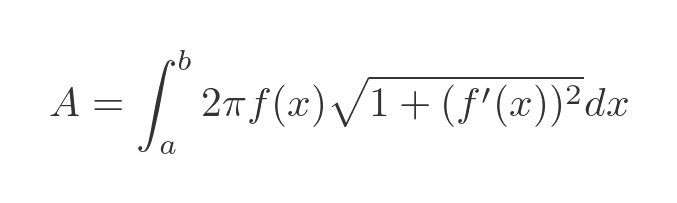
Once again we use the horn function 1/x. This area formula also requires the derivative of 1/x, which is a standard result:

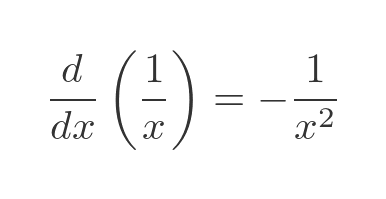
If we substitute f(x) and f'(x) into the integral, we get:

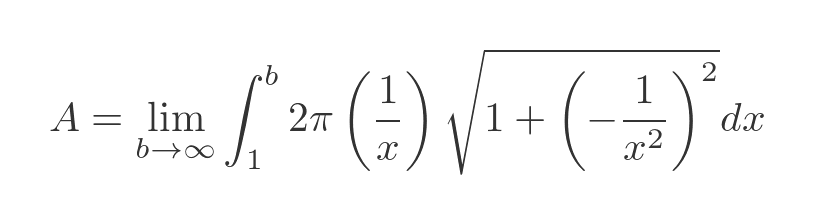
This simplifies to:

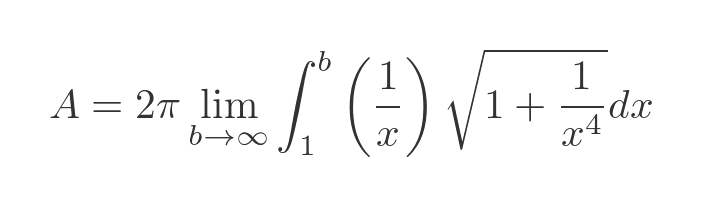
This is not a particularly nice integral to solve, but fortunately, we can sidestep the problem. As with the previous cylinder solution, we are only interested in proving that the integral is infinite. This allows for a neat simplification. Over the interval of interest [1, ∞) this is true:

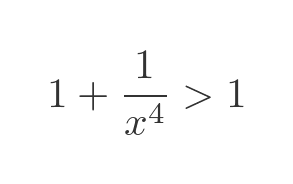
Of course for any number greater than 1, the square root will also be greater than 1:

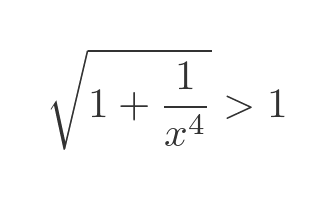
And since 1/x is positive over that interval, this is also true:

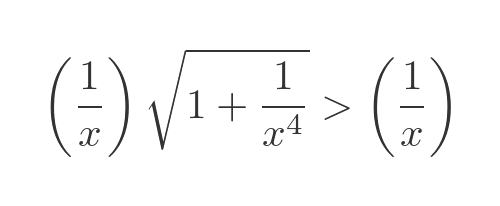
If we replace the square root term with 1 in the original integral, then it will always be less than the surface area:

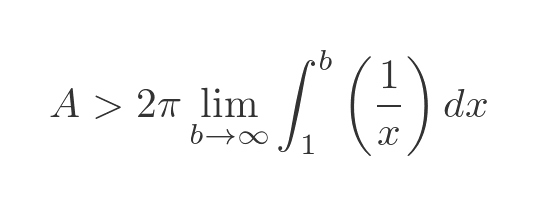
This is useful because we know how to integrate 1/x, it is a standard result, the natural log of x:

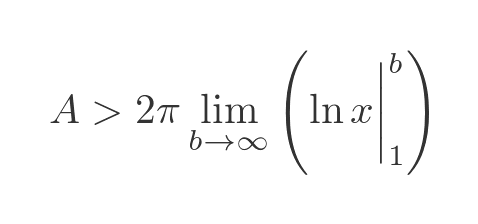
Since ln(1) is 0, the result is just ln(b), which tends to infinity as b increases.

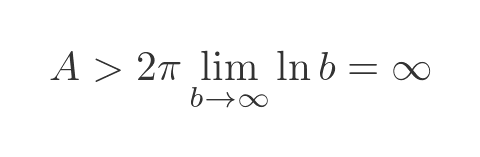
This means that A must also be infinite.

See also

• What is integration
• Integration by substitution
• Mean value theorem for integrals
• Fundamental theorem of calculus
• Improper integrals
• Integration by parts
• Integration by parts - LIATE rule
• Finding arc length by integration
• Volume of revolution