Differentiation - the chain rule

In this article, we will look at using the chain rule to differentiate a composite function.

Composite functions

It is quite common in mathematics to work with composite functions. A composite function takes the form:

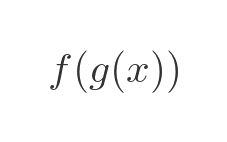
Where f and g are any two functions of a single variable. We call f the outer function, and g the inner function. Combining 2 functions this way is called composing the functions. The result is called a composite function.

We will use this alternative notation for composite functions, as it is a little clearer when we use the chain rule:

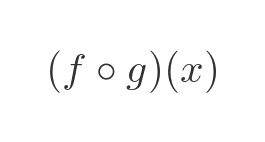
This means exactly the same as the previous notation. We compose f and g, then apply the resulting composite fucntion to the value x,

Examples of composite functions

Here is an example of a composite function, the cosine of x squared:

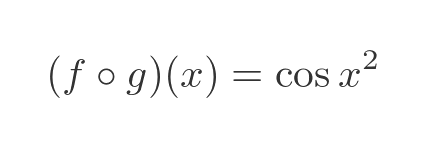
This function is composed of these 2 standard functions:

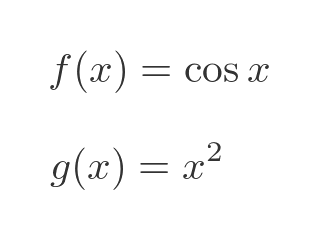
Here is a graph of this function:

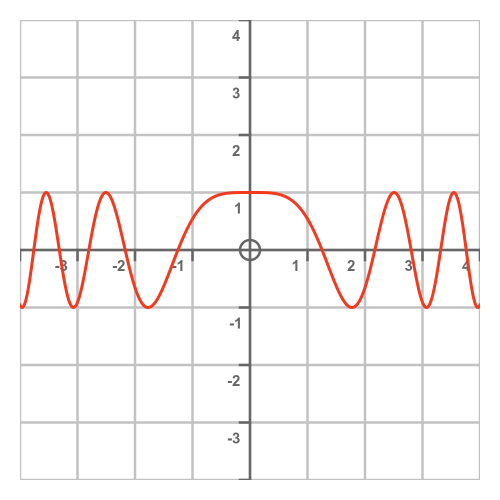
This function is similar to the cosine function, but because the value of x squared changes more rapidly as the magnitude of x gets larger, the cycles of the function get closer together as we get further away from 0.

Here is a second example, e to the power sine of x:

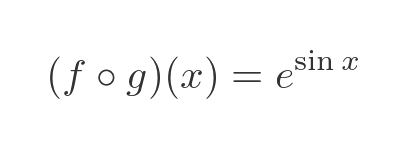
This function is composed of another 2 standard functions:

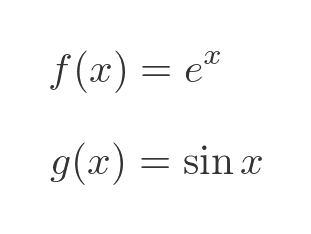
Here is the graph, with the function shown in red (and the sine function shown in grey):

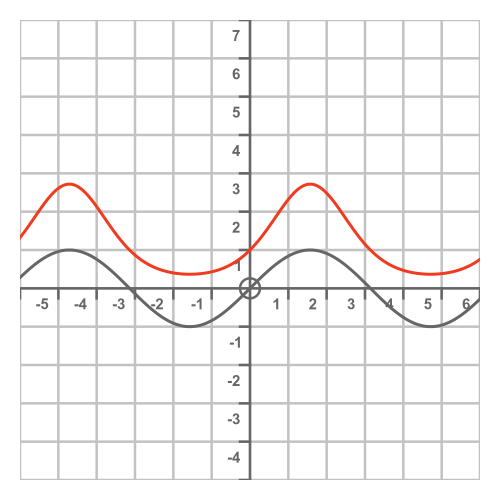
The periodicity of this function is the same as the sine function. The value of the sine function is altered by the exponential function, for example:

• When the sine function has its smallest value, -1, then e to the power sine of x is equal to 1/e (approximately 0.3679).
• When the sine function has its largest value, 1, then e to the power sine of x is equal to e (approximately 2.7183).

The chain rule

How do we differentiate a composite function? Provided f and g themselves are differentiable functions, we can use the chain rule. This can be simply stated as:

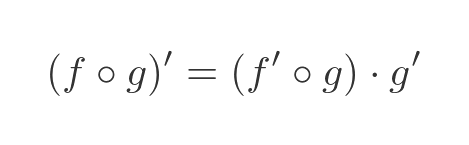
What does this mean?

Well, the first term is f' composed with g. In other words, we find the derivative of f and pass g(x) in as an argument.

The second term is simply g', the derivative of g.

The chain rule tells us that the derivative of f composed with g is the product of the terms above.

We will give some examples below, together with an intuitive explanation of the rule.

Chain rule example 1

Let's see how this works with the first example from before:

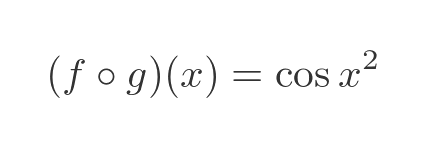
To apply the chain rule we must first differentiate f, and apply it to g. The derivative of cosine is minus sine so when we apply this to x squared we have:

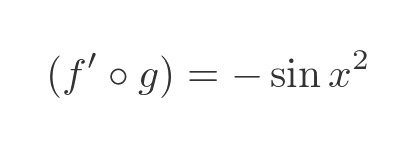
We must then differentiate g. The derivative of x squared is 2x:

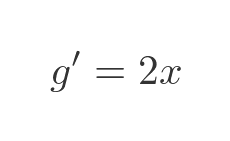
Multiplying the terms gives the derivative of the original composite function:

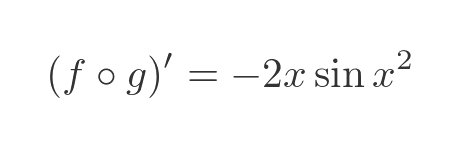
Here is a graph of the original function (left) and its derivative (right). The stationary points of the original function are marked with dots. These correspond to the zero points of derivative, as you would expect:

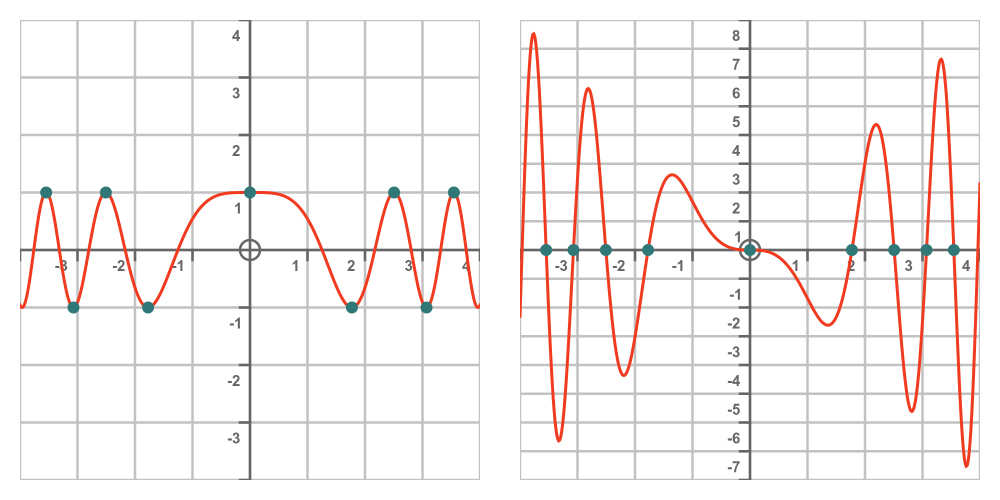
This doesn't prove that the graph on the right is the derivative of the graph on the left, but it is consistent with it being true.

Chain rule example 2

Next, we will look at the second example:

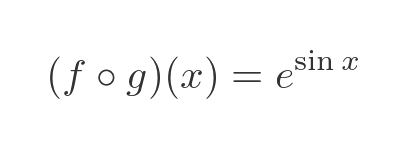
In this case, the derivative of the exponential function f is itself. Applying this to g, the result is the same as the original expression:

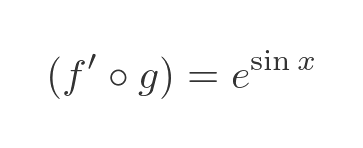
Differentiating the sine term g gives cosine x:

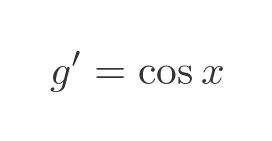
Again we multiply the 2 terms to find the derivative of the original composite function:

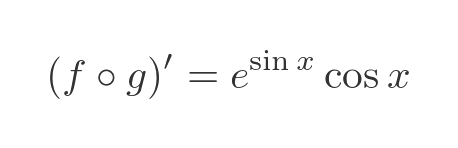
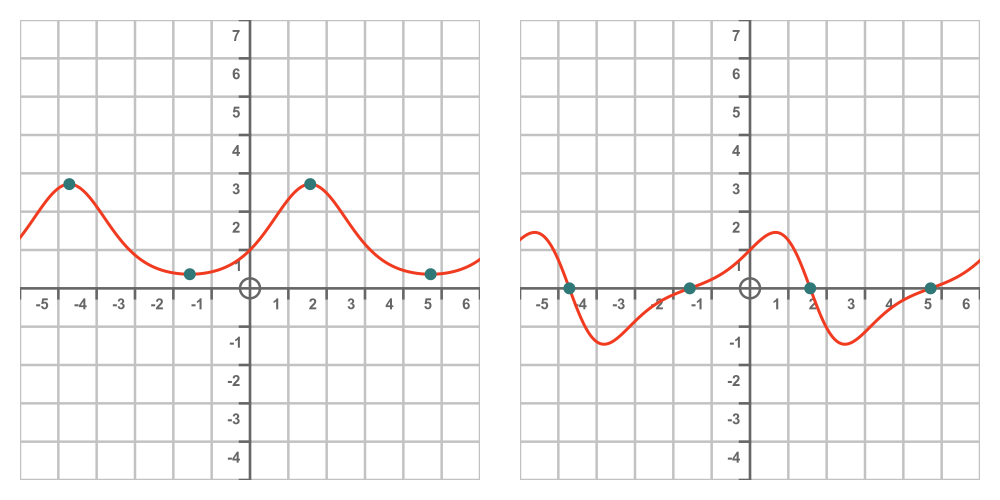
Here is a similar graph of the function (left) and its derivative (right), and again the stationary points are consistent with the zero points of the derivative:

Intuitive explanation of the chain rule

To gain some kind of intuition as to why the chain rule works, let's consider a very simple composite function:

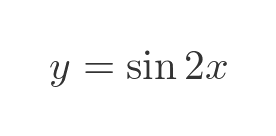
Now let's do a simple substitution, u = 2x:

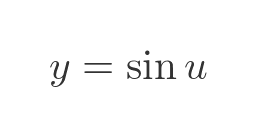
We can differentiate this with respect to u, the result of course is just cosine:

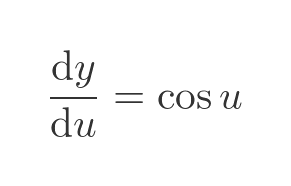
What is the derivative with respect to x? To answer that, here is a graph of sin u and sin x:

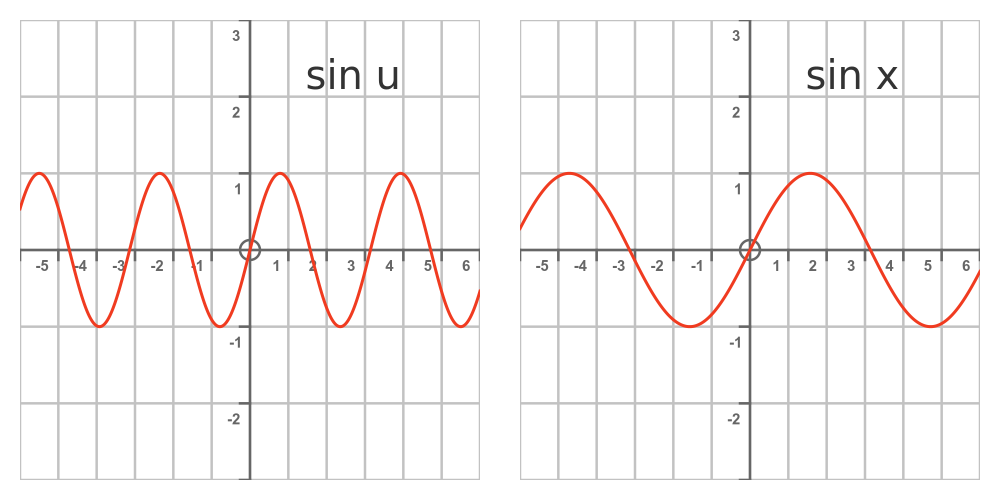
Since u = 2x, the graph of sin u is compressed by a factor of 2 along the x axis - the value of u changes twice as quickly as x.

This in turn means that the slope of the curve sin u is twice the slope of the curve sin x. So we can find the derivative of the curve:

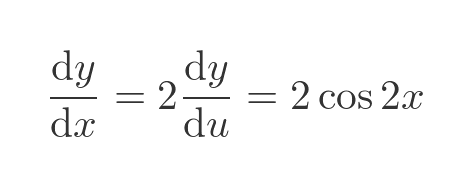
The derivative is multiplied by 2 because u changes twice as quickly as x.

What about a slightly more complex function:

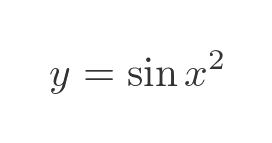
We can do a similar substitution, but this time u is equal to x squared:

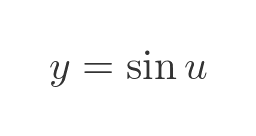
If we differentiate with respect to u we get:

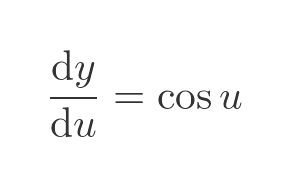
Here is the graph of sin u and sin x:

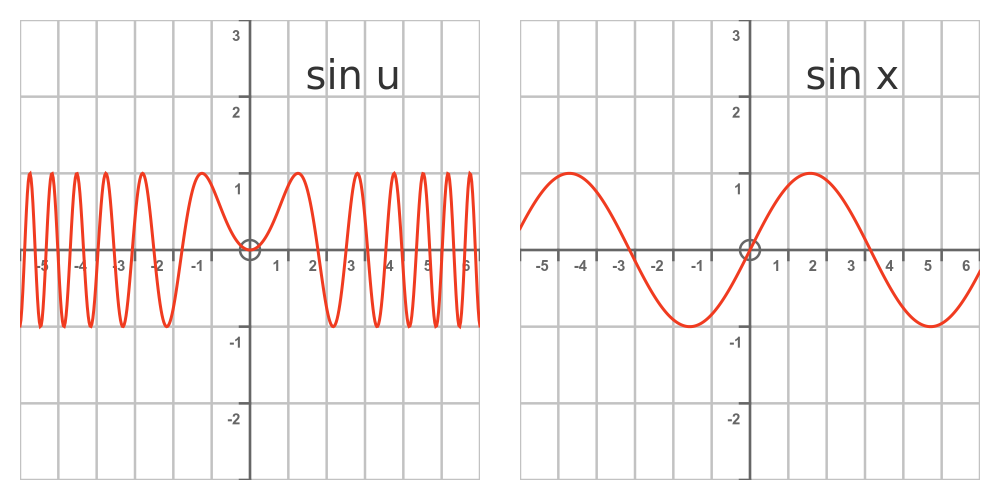
This time the graph gets more and more compressed as x increases. This is because as x increases, the rate of change of u versus x gets faster and faster. So we can't just use a fixed multiplier of 2, we need to find how fast u is changing for any given value of x.

The rate of change of u wrt x, of course, is simply the derivative du/dx. Which in this example is:

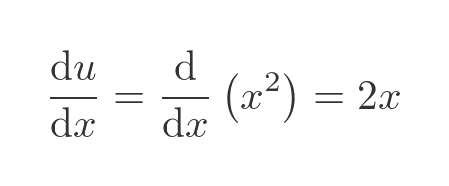
So instead of multiplying by 2 (as we did before), in this example we multiply by 2x:

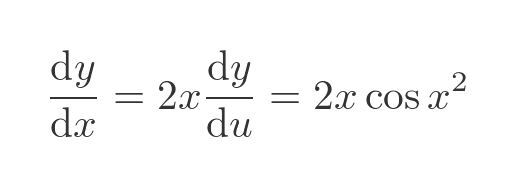
This is identical to the result we would get using the chain rule.

Chain rule and polynomials

Polynomials like this are an interesting example:

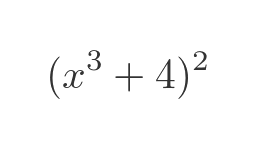
We could differentiate this by first multiplying out the brackets:

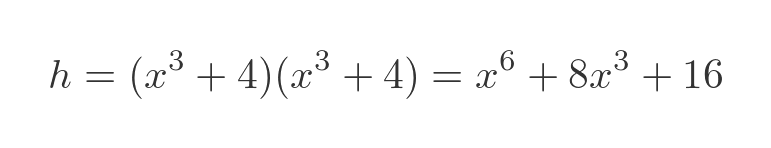
We can then differentiate it in the normal way, giving:

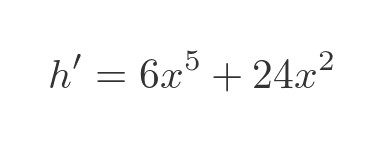
This is ok for a squared term, but if we had a higher power then multiplying out the brackets could be quite tedious. An alternative is to treat it as a composite function and apply the chain rule:

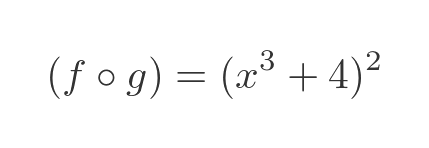
The two functions f and g are:

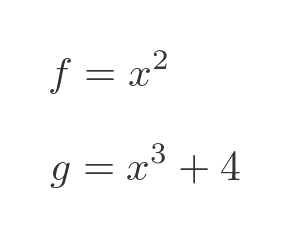
If we differentiate f and compose it with g we get:

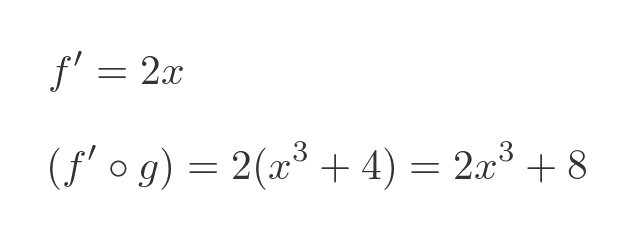
If we differentiate g we get:

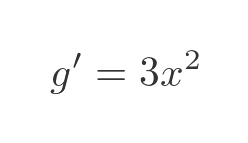
Combining these using the chain rule, in the same way as the previous examples, gives:

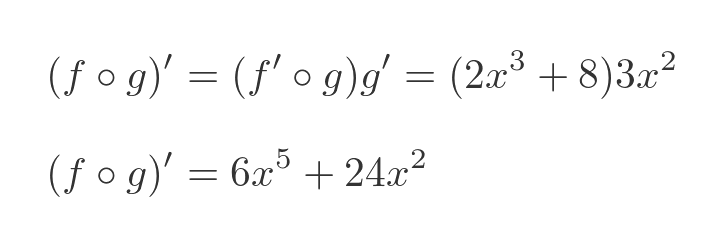
Of course, this gives exactly the same result as the direct differentiation.

See also

• Slope of a curve
• Differentiation from first principles - x²
• Differentiation from first principles - a to the power x
• Second derivative and sketching curves
• Differentiation - the product rule
• Differentiation - the quotient rule
• Differentiation - derivative of an inverse function
• Derivative of sine, geometric proof
• Differentiation - L'Hôpital's rule