Polar curve r proportional to theta
Categories: polar coordinates
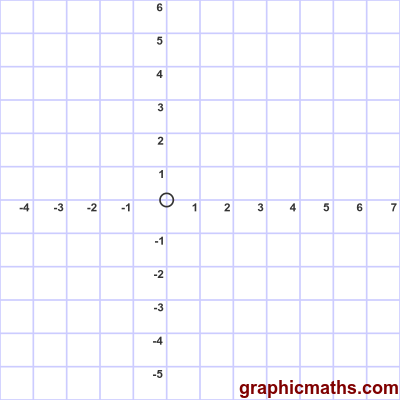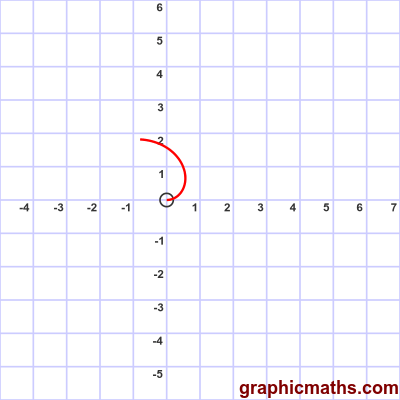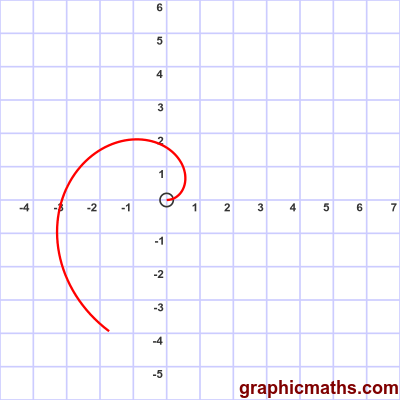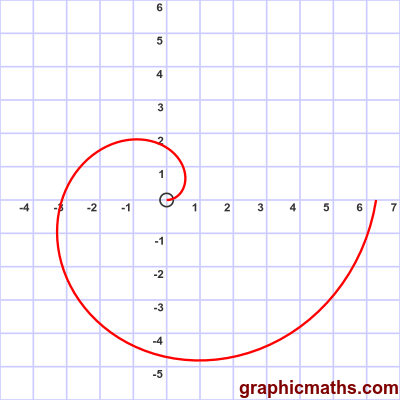
Here is a polar function where $r$ is proportional to $\theta$.
$$r = \theta$$
Describes a curve where $r$ is constant for any angle $\theta$, in this case 3. The curve includes all the points that are a distance of exactly 3 from the origin. This curve, of course, is a circle of radius 3:
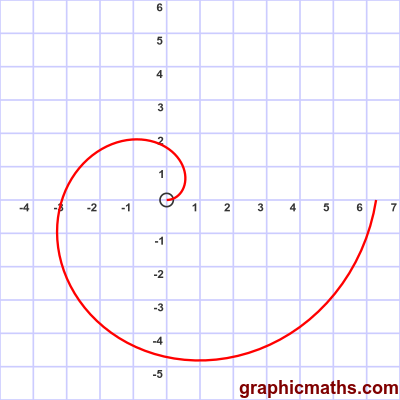
This animation shows how the curve is plotted as $\theta$ moves from 0 to $2\pi$:
Scaling the curve
In general the function:
$$r = a \theta$$
where $a$ is a non-negative constant, describes a spiral curve of that is similar to the curve above (ie it is the same shape, but scaled by $a$). Here are the curves created for $a = 1$ (red), $a = 1/2$ (green), and $a = 1/4$ (blue):
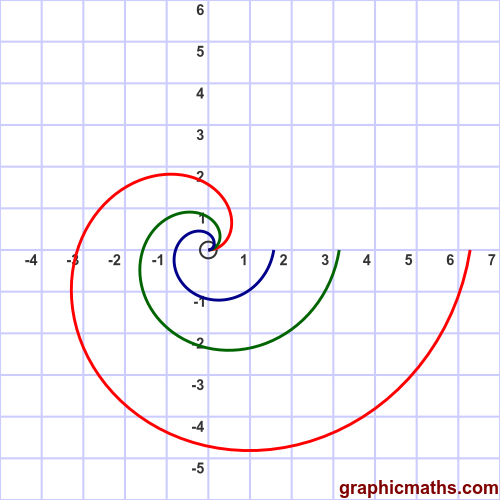
The curve will cross the x-axis at 0, $-a\pi$ and $2 a\pi$. It will cross the y-axis at $a \frac{\pi}{2}$ and $-3 a \frac{\pi}{2}$.
See also
Join the GraphicMaths Newletter
Sign up using this form to receive an email when new content is added:
Popular tags
adder adjacency matrix alu and gate angle area argand diagram binary maths cartesian equation chain rule chord circle cofactor combinations complex modulus complex polygon complex power complex root cosh cosine cosine rule cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon ellipse equilateral triangle eulers formula exponent exponential exterior angle first principles flip-flop focus gabriels horn gradient graph hendecagon heptagon hexagon horizontal hyperbola hyperbolic function hyperbolic functions infinity integration by parts integration by substitution interior angle inverse hyperbolic function inverse matrix irregular polygon isosceles trapezium isosceles triangle kite koch curve l system line integral locus maclaurin series major axis matrix matrix algebra mean minor axis nand gate newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutations polar coordinates polynomial power probability probability distribution product rule pythagoras proof quadrilateral radians radius rectangle regular polygon rhombus root set set-reset flip-flop sine sine rule sinh sloping lines solving equations solving triangles square standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations trapezium triangle turtle graphics variance vertical volume of revolution xnor gate xor gate