Similar triangles proof

The AA and SSS rules for similar triangles were covered here. In this article, we will prove those rules.

Similar triangles

Here are two similar triangles:

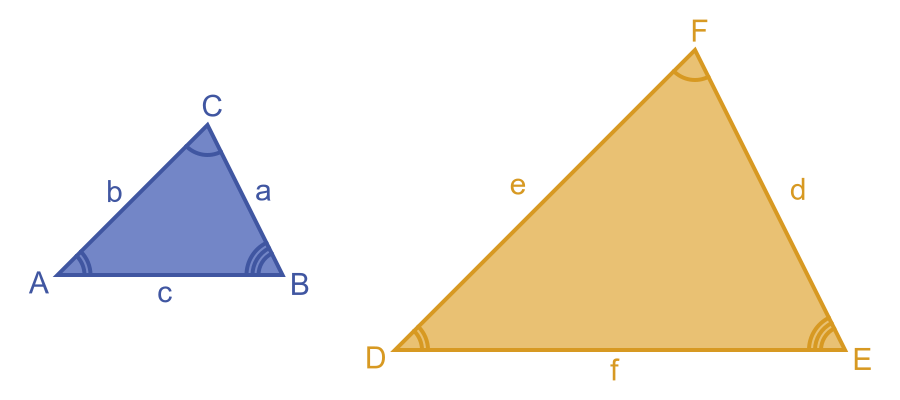
For similar triangles, all corresponding angles are equal:

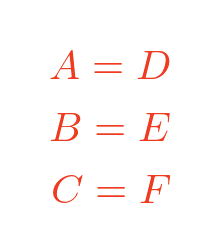
And all corresponding sides are proportionate:

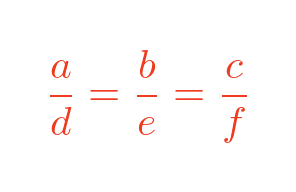
To prove the AA and SSS rules, we need to show that the rules lead to those two conditions.

AA rule

If two triangles have two angles the same, they are similar by the AA rule. We will prove that here.

AA prove all angles are equal

We label the triangles such that these pairs of angles are equal:

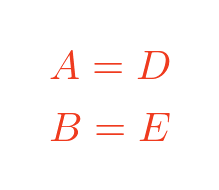
Since the angles in a triangle add up to 180°, we can find C:

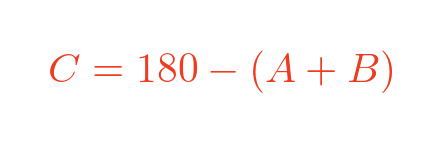
We can also find F:

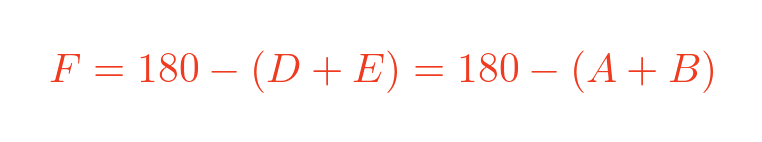
This uses the fact that A = D and B = E. It proves that C = F, so all corresponding angles are equal.

AA prove that all sides are proportionate

Here are the two triangles, redrawn to use the same angles A, B, and C for both triangles:

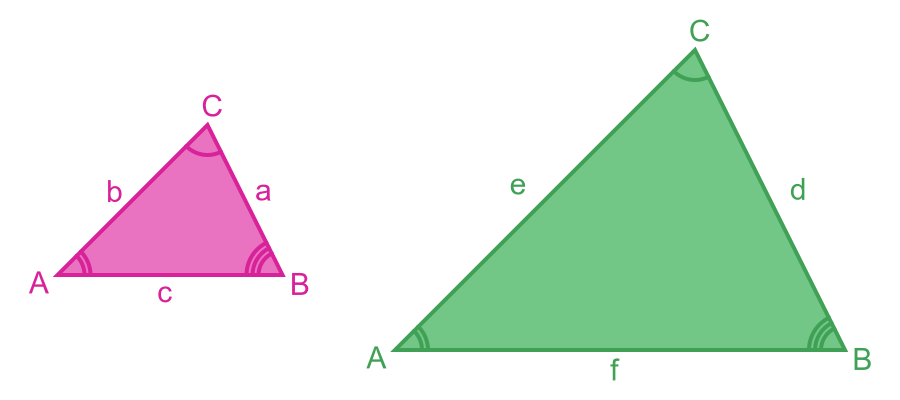
We are going to use the sine rule to prove that the sides are proportionate.

Applying the sine rule to sides a and b of the small triangle:

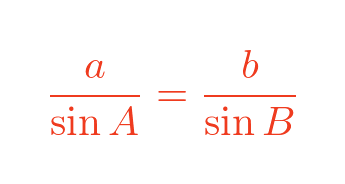
We can rearrange this:

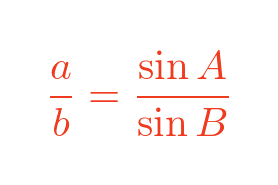
We repeat the same thing for the corresponding sides of the large triangle. Applying the sine rule to sides d and e:

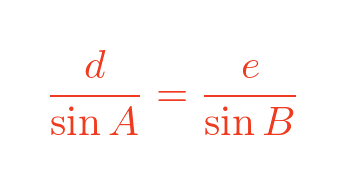
We can rearrange this:

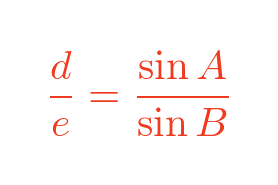
The previous formula for a / b gave the same value, so we know that:

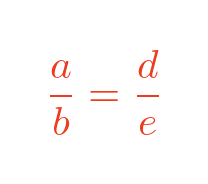
We multiply both sides by b / d:

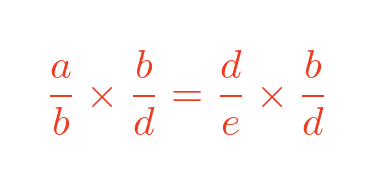
We can then cancel out some terms:

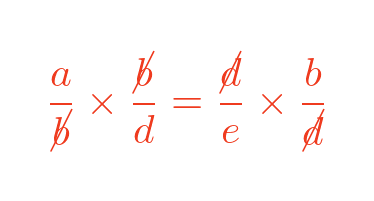
This tells us that sides a and d are in the same proportions as sides b and e:

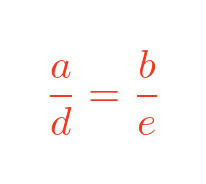
We can do this again using sides a and c of the small triangle (and sides d and f of the large triangle). This results in:

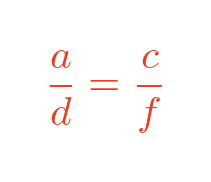
This proves that all corresponding sides are proportionate. So this proves the AA rule.

SSS rule

If two triangles have all corresponding sides that are proportionate, they are similar by the SSS rule. We will prove that next.

This shows the two triangles where the sides are proportional with a scale factor of s. So where small triangle has side a, the large triangle has an equivalent side s times a:

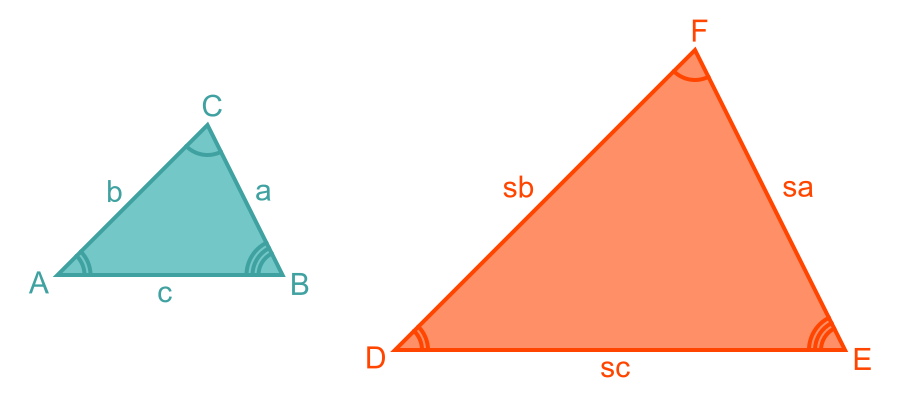
We need to prove that all the corresponding angles are the same. We will use the cosine rule.

We can find the cosine of angle A of the small triangle, using the cosine rule, like this:

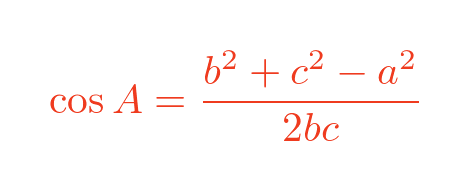
We can also find the cosine of angle D of the large triangle, using the cosine rule, like this:

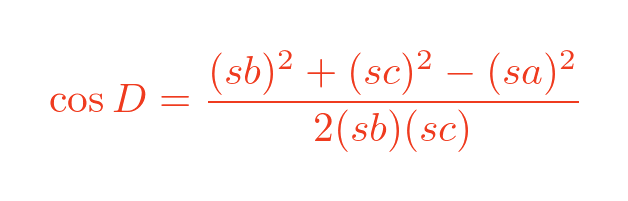
For this triangle we have used s times a instead of a, similar for b and c. We can separate out the terms in s:

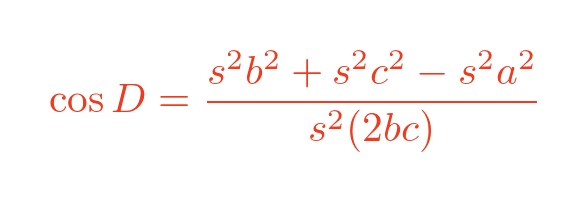
Every term on the top and bottom has a factor of s squared, so we can cancel these out:

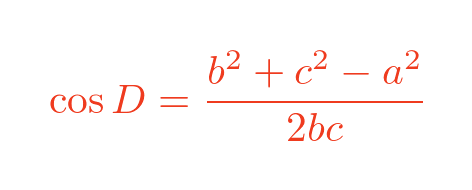
This is exactly the same equation as we had for cos A, proving that angles A and D are the same.

We can use the same steps to prove that angles B and E are the same. And since the angles in a triangle add up to 180° this would then prove that C and F are the same. This proves the SSS rule.

Be careful of inverse trig functions

There is one important point that we have ignored so far in the SSS proof.

Inverse trigonometry functions do not give unique answers.

The cosine of 60° is 0.5. The cosine of 120° is also 0.5. In fact for any angle P:

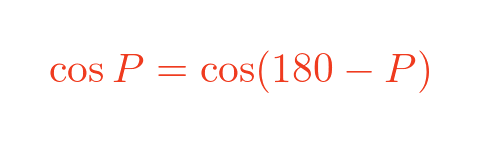
If we know the cosine of P, there will always be an acute angle and an obtuse angle satisfying the condition (unless P is 90° in which case the cosine is 0).

These two triangles illustrate this point:

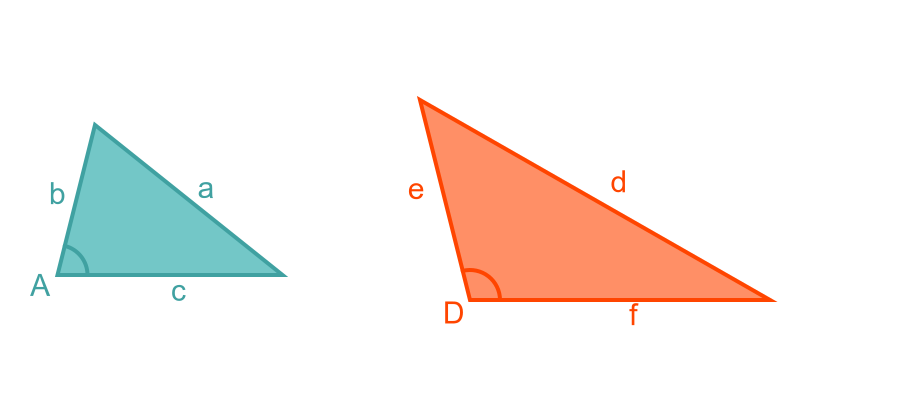
The cosine of A is equal to the cosine of D, but the angles are not the same because clearly one is acute and one is obtuse.

We won't prove it here, but the condition for the angle being acute is:

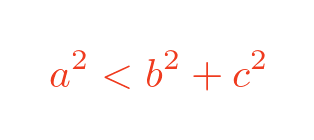
And the condition for the angle being obtuse is:

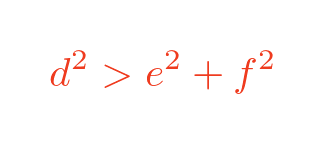
In the case of the SSS rule, we know that the two triangles have sides that are in the same proportions, so it is impossible for one triangle to meet the condition for the angle to be acute and the other to meet the condition for it to be obtuse. So if the cosines are equal, the angles are equal.

See also

• Congruent shapes
• Similar shapes
• Congruent triangles
• Similar triangles