Imaginary and complex numbers

In this article, we will look at imaginary numbers and complex numbers. It serves as an overview, there are links to more in-depth topics.

An imaginary number is a number that, when squared, gives a negative result, for example:

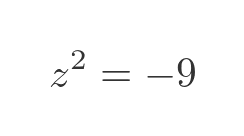
There is no real number that gives this result, since:

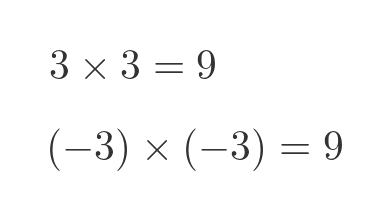
This leads to the idea of a special type of number that, when multiplied by itself, gives a negative result. These are called imaginary numbers, and a combination of a real and imaginary number is called a complex number. Initially, they were regarded as a fairly pointless mathematical oddity. These days, of course, imaginary and complex numbers are important in many branches of maths and science.

Imaginary numbers

An imaginary number is a number that gives a negative result when it is squared. We can define the unit imaginary number as being the number that, when squared, gives -1. In the early days on imaginary numbers, the unit imaginary number was simply written as:

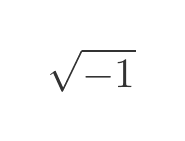
However, this notation leads to an inconsistency. If we take the view that the square of the square root of x is simply x, we get the expected result:

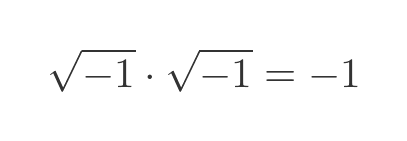
But here is another formula for multiplying square roots:

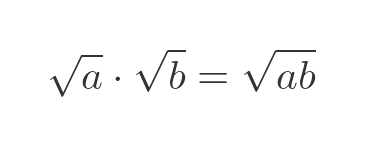
If we apply this second formula to the case when a and b are both equal to -1, we get a different result:

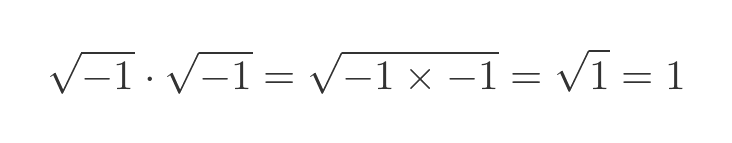
Euler solved this by defining the unit imaginary number i. Squaring i does indeed give -1, but i is not a square root in the normal sense, so it cannot be manipulated as a square root. The second case above doesn't apply so there is no inconsistency.

Any negative square root can be expressed in terms of i, so for example:

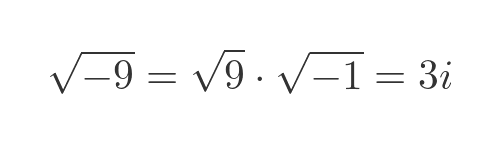
Imaginary numbers exist on a number line, much like the real numbers - but it is a different number line of imaginary values:

Operations on imaginary numbers

We can add two imaginary numbers, like this:

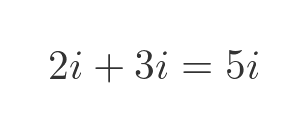
We can also multiply an imaginary number by a real number, like this:

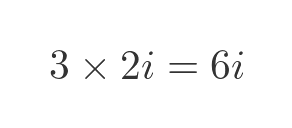
If we multiply an imaginary number by another imaginary number, we must remember that i times i is -1. So we get a real number as a result:

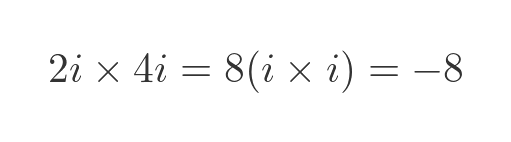
Complex numbers

Real numbers and imaginary numbers are different things, like apples and oranges. If we add 3 apples to 2 oranges, we just have 3 apples and 2 oranges, there is no simpler way to precisely describe it. So if we add a real value 3 to an imaginary value 2i the result is:

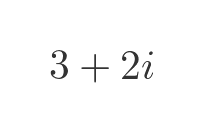
We can't simplify that any further, we have to leave it as the sum of a real number plus an imaginary number. We call this pair a complex number.

If we add 2 complex numbers, we can simplify the result by adding the 2 real parts together and adding the 2 imaginary parts together. But we can't simplify the number any further than that:

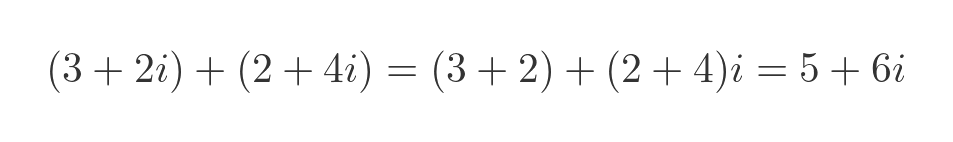
We can also multiply two complex numbers together. We do this by expanding the brackets:

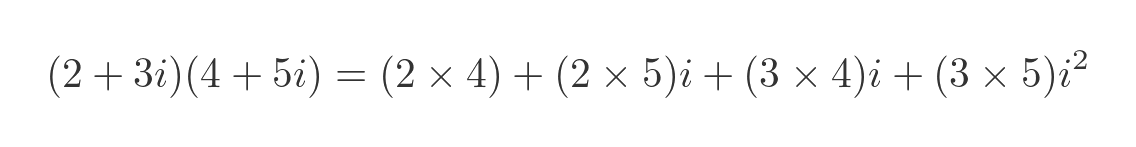
Combining the terms, remembering that i squared is -1, gives:

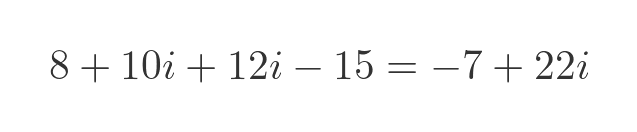
It is also possible to divide complex numbers, see the main article on complex arithmetic.

Argand diagram

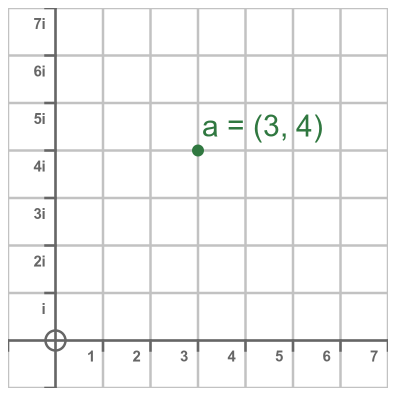
We can think of the 2 parts of a complex number, real and imaginary, as 2 separate number lines, or perhaps 2 axes in a 2-dimensional plane. We call this representation an Argand diagram. The x-axis represents the real part and the y-axis represents the imaginary part. Here is the number 3 + 4i represented as the point (3, 4) on an Argand diagram:

Polar representation

A complex number on an Argand diagram can also be represented in polar coordinates (r, θ). For complex numbers, the radius is normally called the modulus, and the angle is called the argument, so the polar form is called the modulus-argument form of the complex number.

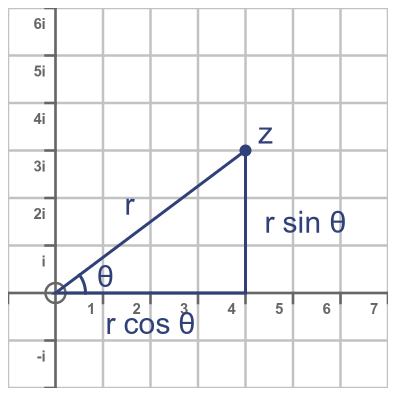
We can write a complex number z in terms of r and θ like this:

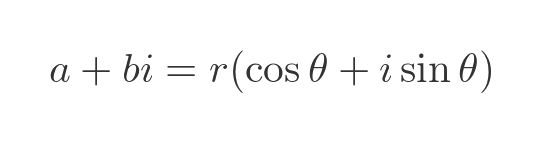
Euler's formula allows us to write the modulus-argument form of a complex number in terms of a complex exponential function:

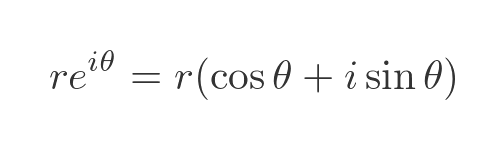
We won't go into detail in this overview, but the complex exponential function operates in a similar way to the real exponential. This means that if we multiply two complex numbers, it adds the arguments (ie the angles) of the two numbers. So complex multiplication has the effect of rotating a number about the origin. Several applications of complex numbers make use of this fact.

Complex functions

We can create complex functions of complex variables. For example, here is a complex polynomial:

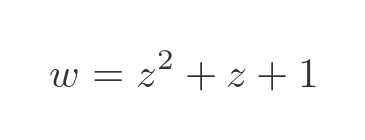
For every complex value z, this function will create a complex value w. This is, effectively, a 4-dimensional curve (2 input dimensions and 2 output dimensions) which makes it difficult to visualise. One way to do this is to create 2 graphs, one showing the real value of w and one showing the imaginary value. Each is shown on the plane of an Argand diagram, using colour to indicate the value at any point. Here is the result for the complex function above:

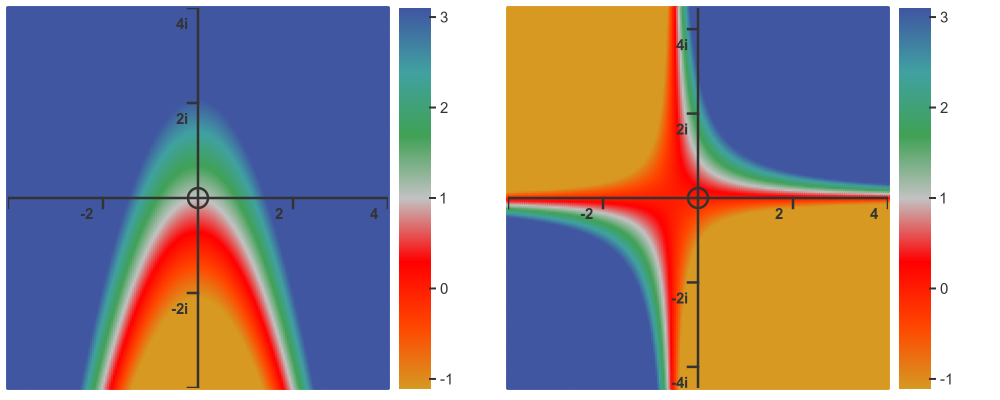
As we saw above, we can define a complex version of the exponential function (Euclid's formula). It is also possible to define complex number versions of sine, cosine, other trig functions, logarithms, hyperbolic functions, and any combination of these.

Applications of complex numbers

Complex numbers now have many practical applications. Here are a few examples.

Complex numbers are often used in the analysis of electric circuits when the voltage varies over time, for example in alternating current circuits, and in analogue electronics. The presence of inductance or capacitance in a time-varying circuit means that it is no longer modelled by Ohm's law alone, it obeys a differential equation. Laplace transforms are often used as a practical way of solving differential equations in that situation.

In signal processing, the Fourier transform is often used to analyse or modify the frequency spectrum of a signal.

In physics, the equations of quantum mechanics are based on complex numbers.

Complex numbers can be used in computer graphics to apply transformations to 2D images. Quaternions, a generalisation of complex numbers, are often used in 3D graphics.

Complex numbers are also used in fractals. For example, the Mandelbrot set and the Newton fractal are based on complex numbers.

See also

• Complex number arithmetic
• Argand diagrams
• Why does complex number multiplication cause rotation?
• Modulus-argument form of complex numbers
• De Moivre's theorem
• i to the power i
• Euler's formula - proof
• Complex powers and roots of complex numbers
• Semiprocal numbers - z to the power i
• Complex polynomials
• Complex number trigonometry functions