Basel problem

In this article, we will take a deep dive into the Basel Problem. The Basel Problem refers to the following infinite series, which has a very strange sum:

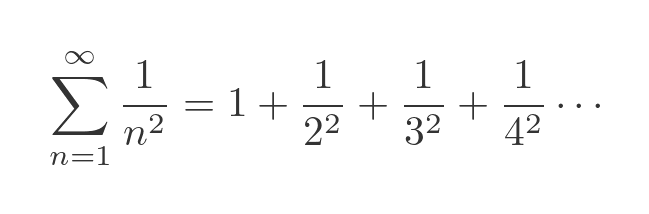
For a long time, it was known that this series converged, and of course, it was possible to calculate the approximate value it converged to, about 1.644934. The challenge was to find a closed form for the solution and to prove it. By closed form we mean an expression involving only mathematical constants and simple functions.

It was Euler who finally came up with a solution, using some very clever (but not too complex) mathematics. This was his first major discovery, and the one that initially made him famous. Since Euler's hometown was Basel, in Switzerland, the problem became known as the Basel problem.

The solution is so unusual that it won't spoil the story too much to reveal it here. The infinite sum converges to pi squared divided by six:

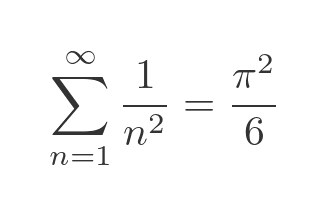
Convergence of the series

The first thing we should address is the question of whether the series actually converges. The terms in the series are:

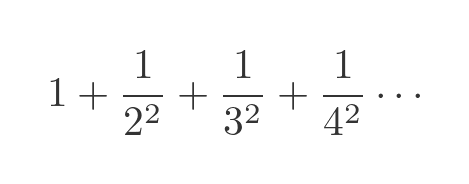
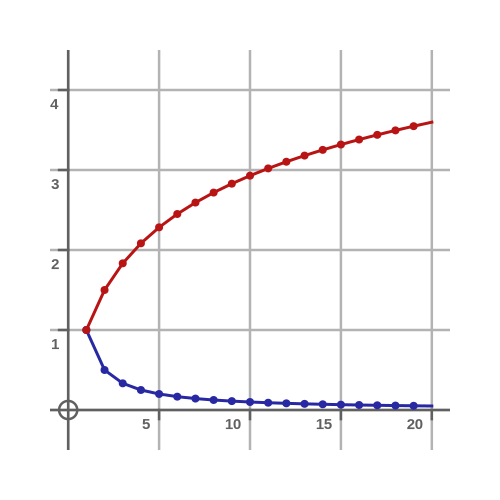
Clearly, these terms get progressively smaller as we continue along the sequence. The graph below shows the values (in blue) and the cumulative total (in red):

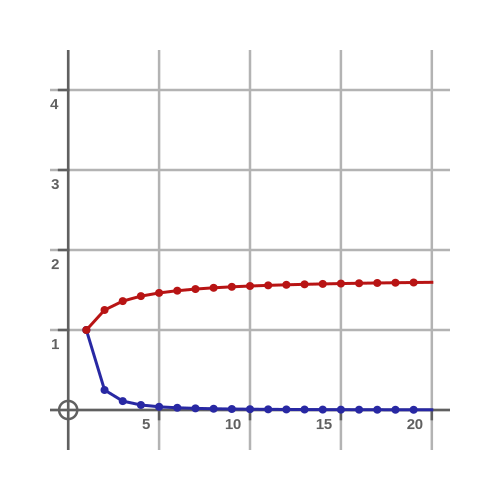
The blue values rapidly fall towards zero as x increases. The red cumulative total appears to approach a limit at around 1.6-ish. This looks like it probably converges.

But we have to be a little bit careful here. The following sequence does not converge, even though the values of the sequence get smaller and smaller:

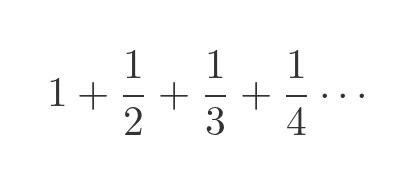
Here is a plot of the values and the cumulative total:

The blue values get smaller and smaller, but not quite as quickly as in the previous case. The slope of the red cumulative total gets smaller and smaller as n increases, but the total still increases without bounds. As n tends to infinity, the cumulative total tends to infinity. It doesn't converge.

What did Euler already know?

Euler used a couple of important results that were known at the time. We will state them here, without proving them. The first was the Maclaurin expansion of the sine function:

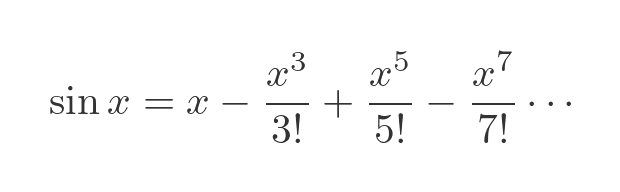
This works for any value of x. The exact value of sin x is given by the sum of an infinite number of terms. However, the terms get smaller and smaller as we move from left to right, so we can find a good approximation to sin x simply by using enough terms.

The second result is this one limit:

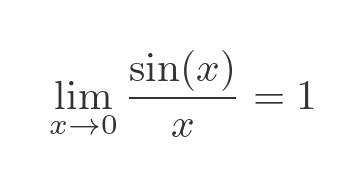
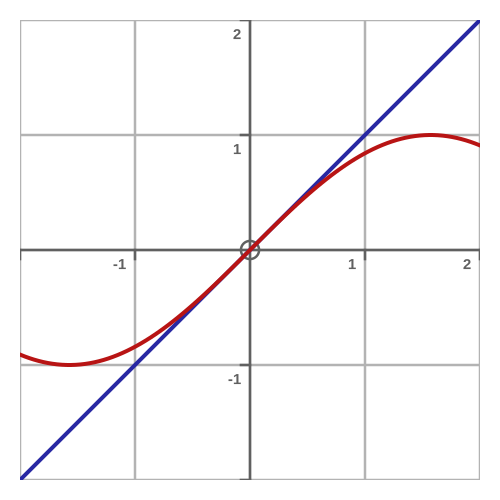
For most values of x, it is easy to calculate sin(x)/x. But when x is 0, both sin(x) and x are 0. Fortunately, it can be shown that the limit as x tends to 0 is 1. This is often proved using the squeeze theorem. This graph illustrates the result, showing that as x approaches 0, the graphs of sin x (in red) and x (in blue) become close to identical, so their ratio will approach 1:

Expressing sin x as a product of terms

A polynomial with distinct, real roots can be written as a product. For example, a cubic equation with roots a, b, and c can be written as:

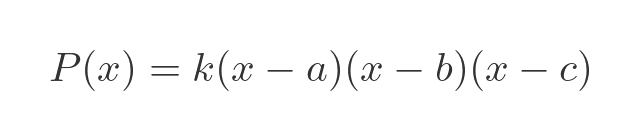
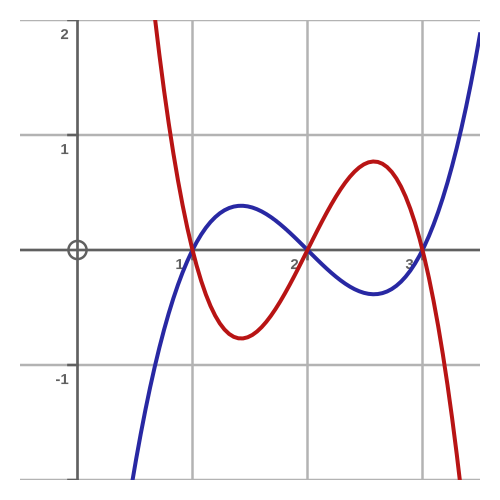
This function has roots at a, b, and c. For example, when x = a, the term (x - a) is 0, so the whole function is 0. The factor of k reflects the fact that there are infinitely many different cubic curves with roots a, b, and c, that are all the same basic shape but scaled in the y direction. This plot shows the polynomial above, with k values of 1 (blue) and -2 (red). Both curves cross the x-axis at 1, 2 and 3 (the roots) but have different values everywhere else:

Euler's breakthrough was to extend this concept. What if a polynomial had infinitely many roots? Could that be represented as an infinite product? If so, perhaps we could express the sine function in that way. We know that:

• The sine function can be expressed as a polynomial, a Maclaurin expansion.
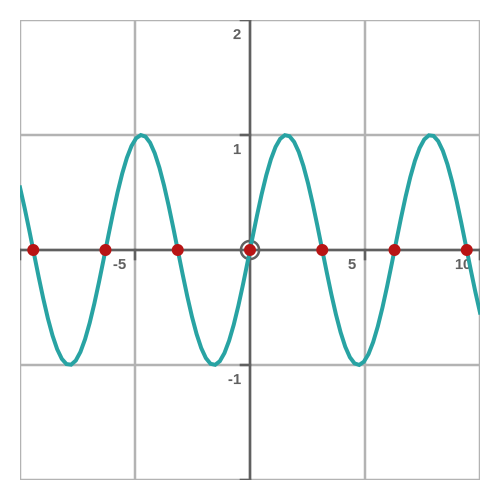
• The sine function has roots at 0, π, 2π, 3π ...
• It also has roots at -π, -2π, -3π ...

This graph shows the sine function, with the roots mentioned above shown as red dots:

Euler reasons that we should be able to write the sine function as:

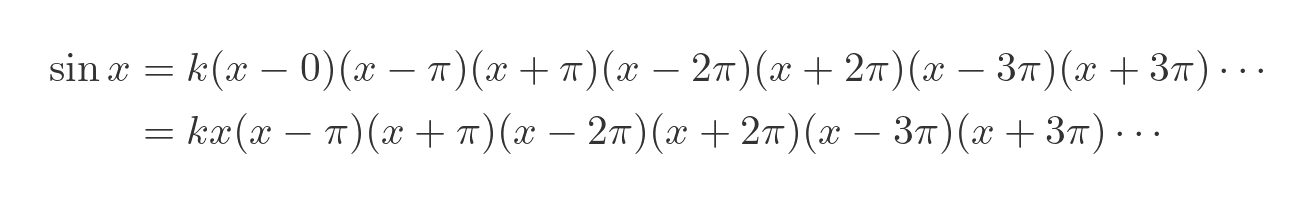
Notice we have paired the roots. The term (x - π) represents the root at π, the term (x + π) represents the root at -π, and so on. The term (x - 0), or simply x, represents the root at 0.

It was another 100 years until Weierstrass formally proved the validity of this expansion, but we will see a fairly solid justification for it shortly.

Now let's simplify the equation above. We can combine each pair of positive and negative roots by multiplying the brackets. This is just the difference of squares factorisation:

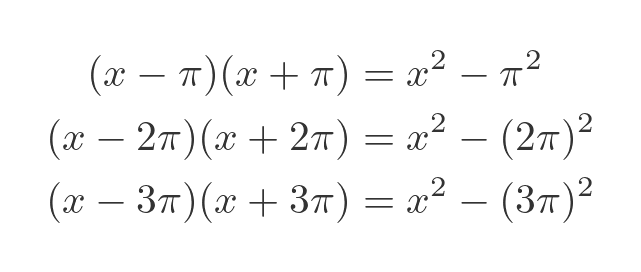
Replacing each pair of terms in the original formula for sin x gives this result:

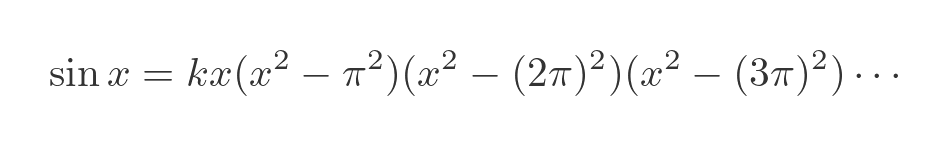
Finding k

We now need to find the value of k. In the previous formula, any non-zero value of k will give us a polynomial that has a root at every integer multiple of π, but for that function to be identical to the sine function, we need to choose the correct value for k. Let's start by isolating k:

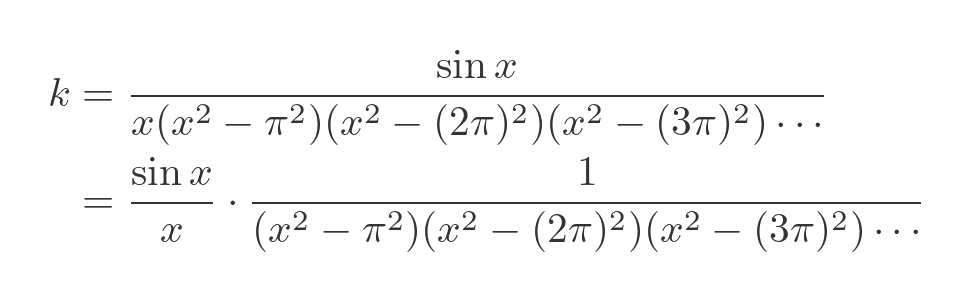
We have separated out the term sin(x)/x, which will be useful in the next step.

Since k is a constant, the above formula is true for any value of x. If we evaluate it in the limit as x tends to zero, all the terms in x squared will disappear, which makes things a lot simpler. Also remember that, as x tends to 0, sin(x)/x tends to 1. So the expression for k becomes:

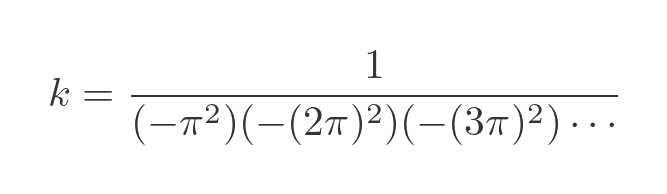
So now let's put our newly discovered value for k back into the previous equation for sin x:

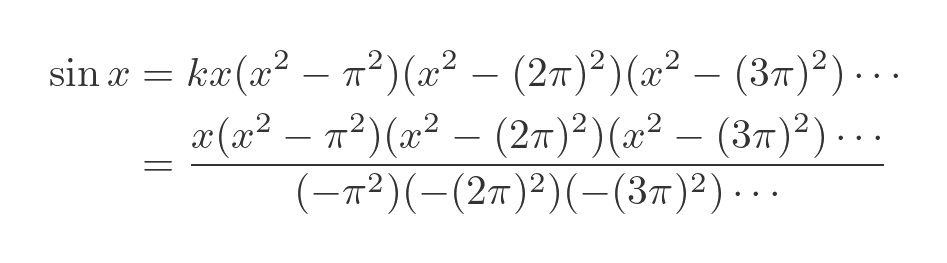
Sanity check - is this function really sin x?

There is a slight problem with the formula above. Look at the factors in the denominator: -π², -(2π)², -(3π)²... They get bigger and bigger in magnitude, without limit. Their product is infinite. Similarly, for any particular value of x, the factors in the numerator grow in magnitude without limit. We are dividing infinity by infinity, and somehow the result is the sine function? How can we be sure that is valid?

Well, the important thing to notice here is that every factor on the bottom has an equivalent factor on the top. That is to say, for each factor in nπ on the bottom, there is a factor in nπ on top. Here is the same formula, but written with the corresponding factors grouped together inside brackets:

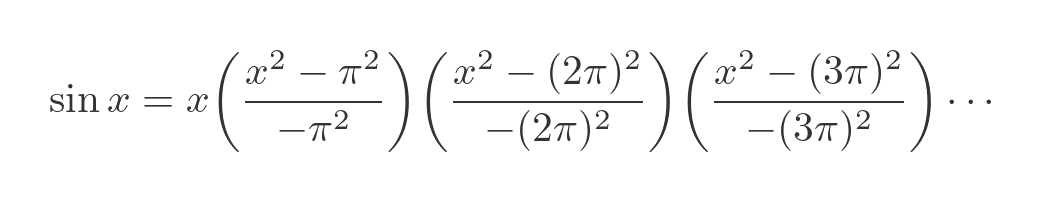
We can simplify this further by applying a simple algebraic manipulation:

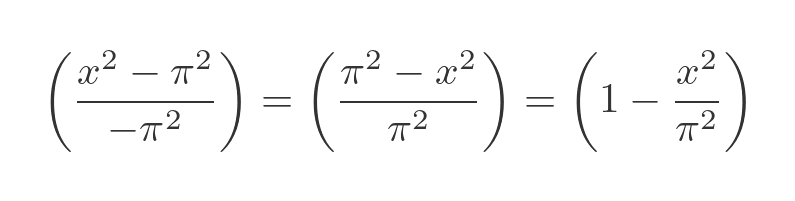
Applying an equivalent manipulation to every factor gives:

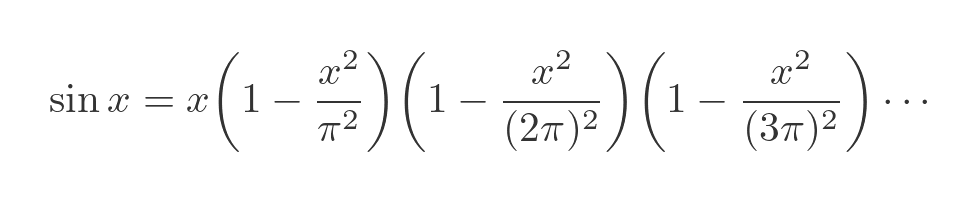
Let's evaluate this for some value of x, say 1 (it doesn't matter what value we choose). Here are the first few factors:

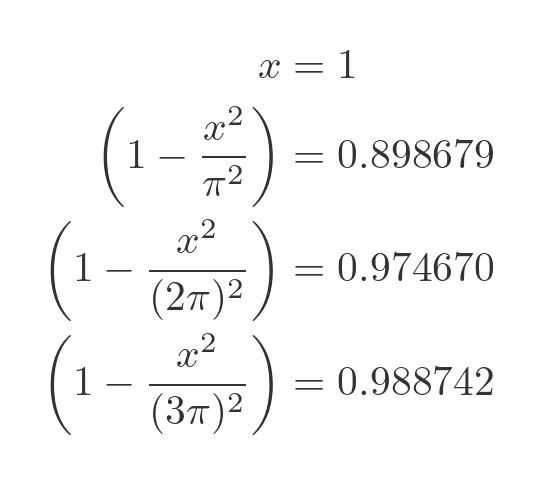
Notice that each factor gets closer and closer to 1. That is because in each factor, the denominator of the fraction gets larger, so the fraction gets smaller, so the entire factor gets closer to 1.

This is important because the closer a factor gets to 1, the less effect that factor has on the overall result. So, factors that are much later in the product will have a negligible effect. This doesn't prove that the product will converge, but it gives us some confidence that it might. In addition, unlike Euler, we now have computers that can calculate these products very quickly and plot a graph:

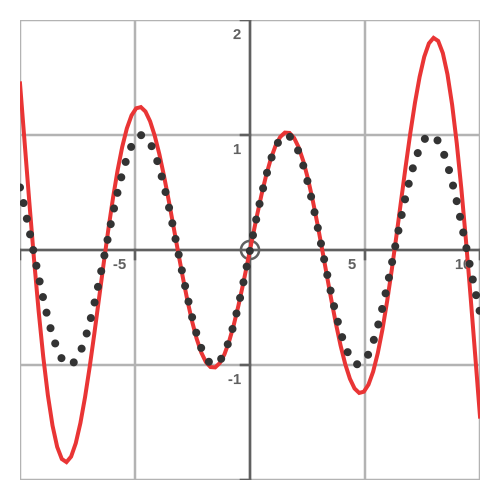
The red plot uses the function above, with the first 10 factors calculated. The black, dotted line is the sine function. As we can see, the red plot follows the sine curve reasonably accurately for values of x in the range of about +/-4. Beyond that range, it becomes increasingly inaccurate. We won't pursue this any further here, but we can make the function accurate over a much longer range by increasing the number of factors we calculate.

Solving the Basel problem

This has been such a long detour that you could be forgiven if you have forgotten what we are actually trying to do. But now let's bring everything together.

We have two different polynomial expressions for the sine function. The Maclaurin expansion:

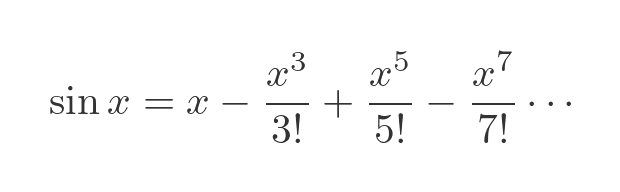
And the product formula we have just derived:

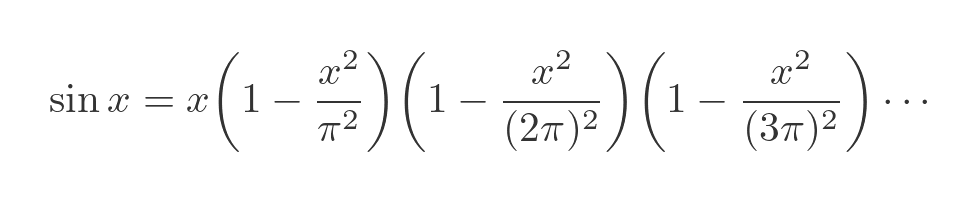
Now, since these two polynomials are indeed the same function, we know that each corresponding term in both polynomials must be the same. We will concentrate on the x-cubed term. Starting with the product formula, we have an initial x term multiplied by an infinite number of brackets. If we can find the x-squared term of the product of the brackets, then when we multiply it by the initial x, we will have the x-cubed term for the whole expression.

How do we multiply an infinite number of brackets? In general, that can be tricky, but in the specific case of finding the x-squared term, it is quite easy. It is the sum of:

• The x-squared term from the first set of brackets, multiplied by the ones in all the other brackets.
• The x-squared term from the second set of brackets, multiplied by the ones in all the other brackets.
• And so on.

Here is the complete x-cubed term for the series (notice that all the terms are negative, because all the original terms in x-squared are negative):

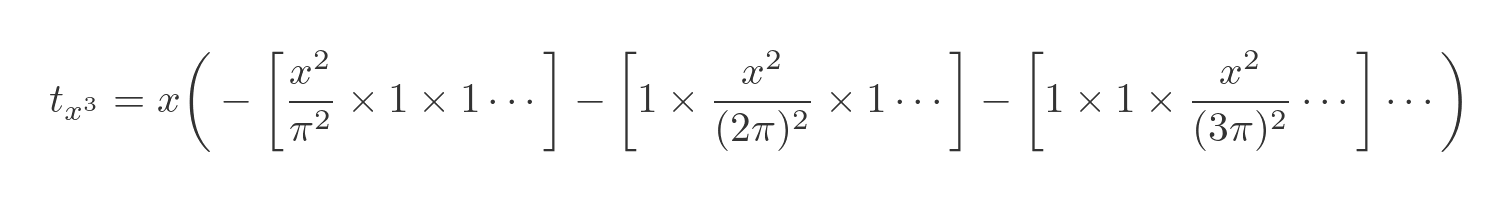
We can simplify this, first by cancelling all the multiplications by 1, and then by taking out the common factor of x²/π²:

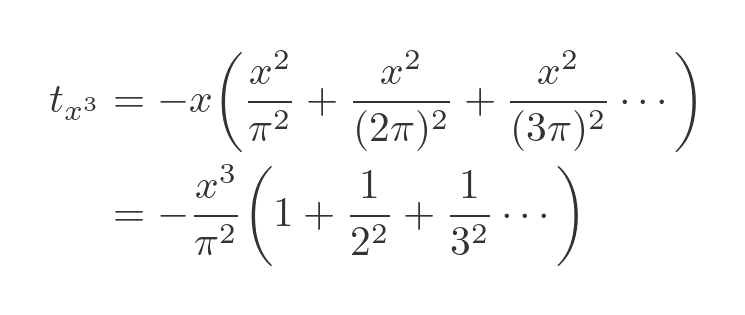
This looks very promising! The infinite series in the brackets is the Basel problem series, and there is even a π² term there.

The final step is to equate this term to the x-cubed term in the Maclaurin expansion. As we noted, if those two polynomials both represent the sine function, then every corresponding term in both polynomials must be equal. The x-cubed term in the Maclaurin series is:

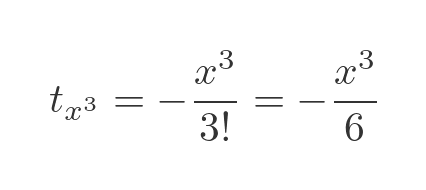
Equating this with the previous term gives:

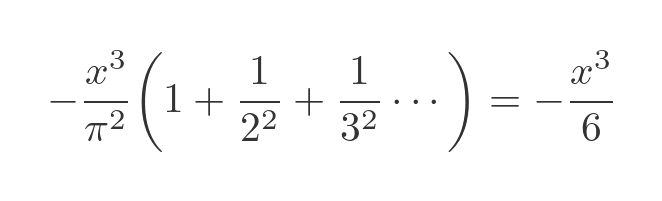
Cancelling the negative and the x-cubed term, and rearranging slightly gives:

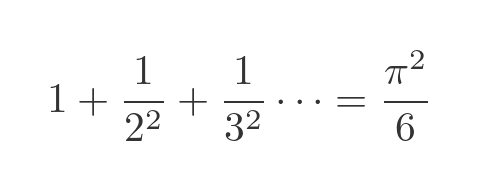
Which solves the Basel problem!

Did Euler guess the answer beforehand?

Euler knew the approximate value of the sum to quite a few decimal places. It is certainly possible that he guessed the number was π²/6. Having guessed the value, it would have been easy to verify it to many decimal places, which would have given a very strong indication (but not a proof) that it was correct.

At the time, the Leibniz formula for pi was already known:

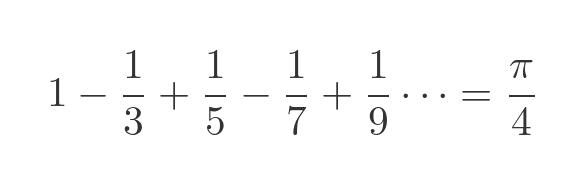
It isn't beyond the bounds of possibility that Euler might have wondered if an infinite sum of squares might be a simple multiple of π². Still, there doesn't seem to be any hard evidence that he guessed the result in advance. Not that it really makes any difference, the proof is still very clever, and knowing the result wouldn't have helped very much. Mathematicians are allowed to guess the answer before they start! Provided the final proof is valid, it doesn't matter how you got there.

Is this a valid proof?

This proof was brilliant in its time, but doesn't quite meet modern standards of a rigorous mathematical proof.

The step where Euler expressed the sine function as a product of an infinite number of terms was not formally proven, and as mentioned above, it was quite some time before Weierstrass formally proved it (and also showed that, though it works for sine, it doesn't work for all functions). So Euler was correct, but his proof was not completely watertight.

But of course, he had very good reason to think it was true. The result of manually calculating the series, to many decimal places, exactly agreed with the result of calculating π²/6 to many decimal places. And as we have seen, the graph of the function looks exactly like the graph of the sine function (and even more so if we calculate to a lot more than 10 terms).